10.5.2 Hraničné podmienky

Pri odvodení podmienok pre magnetickú indukciu B a intenzitu magnetického poľa H pri prechode cez rozhranie medzi dvomi prostrediami s rôznymi magnetickými vlastnosťami budú východiskom dva integrálne zákony magnetického poľa - Gaussova veta (10.5.1.3) a Ampérov zákon celkového prúdu (10.4.2.10).

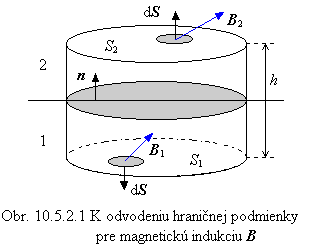
Uvažujme, že Gaussov uzavretý povrch má tvar povrchu valca. Spodná podstava sa nachádza pod rozhraním v prostredí 1, vrchná podstava sa nachádza nad rozhraním v prostredí 2. Obe podstavy s plošným obsahom S₁ = S₂ = S sú rovnobežné s rozhraním a povrch plášťa s plošným obsahom S_p je na rozhranie kolmý. Nech jednotkový normálový vektor n je kolmý na rozhranie a je nasmerovaný z prostredia 1 do prostredia 2, pozri obr. 10.5.2.1.

Z Gaussovej vety pre uzavretý povrch valca S_v vyplýva

Pri posúvaní podstáv k rozhraniu (h®0) zrejme S_p®0. Ak nie je magnetická indukcia B na povrchu plášťa neobmedzene veľká, pri S_p®0 konverguje magnetický tok cez povrch plášťa k nule. V limitnom prechode S_p®0 získame

Pri integrovaní sme predpokladali, že podstavy valca sú natoľko malé, aby príslušná magnetická indukcia bola v každom bode svojej podstavy rovnaká. Z posledného vzťahu vyplýva hraničná podmienka pre magnetickú indukciu B

(10.5.2.1)

To znamená, že pri prechode z jedného prostredia do druhého sa nemení normálová súradnica (kolmá zložka) magnetickej indukcie B

(10.5.2.2)

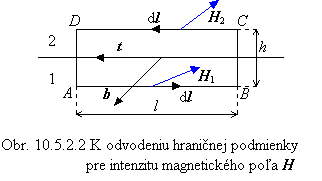
Uvažujme teraz o uzavretej orientovanej krivke ABCDA v tvare obdĺžnika ohraničujúceho povrch s plošným obsahom S. Spodná strana sa nachádza pod rozhraním v prostredí 1, vrchná strana sa nachádza nad rozhraním v prostredí 2. Obe strany sú rovnobežné s rozhraním a majú dĺžku l₁=l₂=l. Bočné strany majú výšku h. Nech jednotkový vektor t leží na povrchu obdĺžnika a súčasne na rozhraní prostredí. Nech jednotkový vektor b je kolmý na povrch obdĺžnika a jeho smer je vybraný pravidlom pravej ruky vzhľadom na orientovaný obvod obdĺžnika, pozri obr. 10.5.2.2.

Z Ampérovho zákona celkového prúdu (10.4.2.10) pre uzavretý obvod l_o obdĺžnika vyplýva

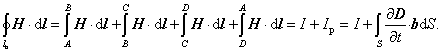
Pri posúvaní vodorovných strán k rozhraniu (h®0) zrejme S®0. Ak nie je časová derivácia elektrickej indukcie D v bodoch povrchu S neobmedzene veľká a taktiež ak je obmedzená intenzita magnetického poľa H na bočných stranách obdĺžnika, potom pri S®0, h®0 konvergujú Maxwellov posuvný prúd I_p cez povrch S a integrály intenzity magnetického poľa H po bočných stranách obdĺžnika k nule. V limitnom prechode S®0, h®0 získame

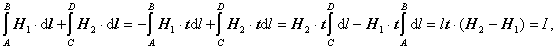
kde vodivostný elektrický prúd I tečie po rozhraní cez úsečku dĺžky l. Pri integrovaní sme predpokladali, že sú vodorovné strany obdĺžnika také malé, aby príslušná intenzita magnetického poľa bola v každom bode svojej strany rovnaká. Z posledného vzťahu vyplýva

(10.5.2.3)

kde j_l je lineárna hustota elektrického prúdu na rozhraní, j_lb je jej súradnica do smeru vektora b.

Ak po rozhraní netečie elektrický prúd (j_l = 0), potom sa pri prechode z jedného prostredia do druhého nemení dotyčnicová súradnica (rovnobežná zložka) intenzity magnetického poľa H

(10.5.2.4)

Jednotkový vektor t vo vzťahu (10.5.2.3) môžeme vyjadriť ako vektorový súčin vektora b a normálového vektora n (pozri obr. 10.5.2.1), preto po dosadení do (10.5.2.3) a úprave dostaneme

Pretože posledný vzťah platí pre ľubovoľný vektor b rovnobežný s rozhraním, musí platiť hraničná podmienka pre intenzitu magnetického poľa H

(10.5.2.5)

Príklad 10.5.2.1

Vypočítajte veľkosť a smer magnetickej indukcie B₂ v druhom prostredí, ak magnetická indukcia B₁ v prvom prostredí zviera s normálovým vektorom na rozhranie uhol b₁ = 45° a jej veľkosť je B₁ = 10 mT! Prvým prostredím je vzduch, relatívna permeabilita druhého prostredia je m_r2 = 10. Prostredia sú homogénne a izotropné. Po rozhraní medzi prostrediami netečie žiadny elektrický prúd.

Riešenie:

Homogénne prostredie má v každom bode rovnakú permeabilitu. Ak permeabilita nezávisí od smeru magnetizácie, prostredie je izotropné. Prvým prostredím je vzduch, preto označme m_r1 = 1. S využitím (10.5.2.2) a (10.5.2.4) pre pomer tangensov uhla lomu b₂ a uhla dopadu b₁ magnetickej indukčnej čiary pri prechode cez rozhranie, po ktorom netečie elektrický prúd, dostaneme tzv. zákon lomu magnetickej indukčnej čiary

Úpravou a dosadením vypočítame uhol b₂, ktorý zviera magnetická indukcia B₂ s normálovým vektorom

Z pravouhlej trigonometrie s využitím (10.5.2.2) úpravou a dosadením vypočítame veľkosť magnetickej indukcie v druhom prostredí

Magnetická indukcia B₂ v druhom prostredí má veľkosť 71,07 mT a zviera uhol 84,29° s normálovým vektorom.

Kontrolné otázky:

1. Definujte magnetický tok a vyslovte Gaussovu vetu pre magnetický tok!

2. Sú magnetické indukčné čiary vždy uzavreté?

3. Postulujte 3. Maxwellovu rovnicu!

4. Zakreslite magnetické indukčné čiary pre priamy prúdovodič, pre cievku s prúdom a pre trvalý magnet!

5. Aké znamienko má magnetický tok vychádzajúci von časťou uzavretého povrchu?

6. Prečo je 4. Maxwellova rovnica pre stacionárne magnetické pole jednoduchšia než pre nestacionárne magnetické pole?

7. Ak po rozhraní dvoch rôznych magnetík tečie elektrický prúd, mení sa normálová súradnica magnetickej indukcie B alebo nie?

8. Objasnite hraničnú podmienku pre intenzitu magnetického poľa H.

Úlohy:

1. Vypočítajte veľkosť a smer intenzity magnetického poľa v druhom prostredí, ak intenzita magnetického poľa H₁ v prvom prostredí zviera s normálovým vektorom na rozhranie uhol b₁ = 45° a jej veľkosť je H₁ = 10 A.m^-1! Prvým prostredím je vzduch, relatívna permeabilita druhého prostredia je m_r2 = 500. Prostredia sú homogénne a izotropné. Po rozhraní medzi prostrediami netečie žiadny elektrický prúd. (H₂ = 0 A.m^-1, b₂ = 0°)

2. Vypočítajte intenzitu magnetického poľa na povrchu nekonečne dlhého priameho medeného vodiča s jednosmerným prúdom I = 2 A. Vodič sa nachádza vo vákuu. Má kruhový prierez polomeru R = 1 cm. Ako sa zmení magnetická indukcia pri prechode cez rozhranie medzi medeným vodičom (1) a vákuom (2)? Meď je diamagnetická s relatívnou permeabilitou m_r1 = 0,9999904. Elektrický prúd na povrchu vodiča neuvažujte. (H=31,831 A.m^-1, B₁=39,9996 mT, B₂=40,0000 mT)

3. Odvoďte vzťah pre magnetický tok cez povrch obdĺžnika so stranami dĺžky a, b, ak je nekonečne dlhý priamy vodič s elektrickým prúdom I uložený vedľa obdĺžnika v rovine obdĺžnika rovnobežne so stranami dĺžky a. Vzdialenosť vodiča od najbližšej strany obdĺžnika je R. Vodič aj obdĺžnik sa nachádzajú vo vákuu. (F=(m₀Ia/2p).ln(1+b/R))