13.1.4 Experimentálny dôkaz hybnosti elektrónu – Comptonov jav

Max Planck postuloval vyžarovanie energie po kvantách v jednotkách hf . Albert Einstien rozšíril postupne túto teóriu o skutočnosti:

· energia sa nielen vyžaruje ale aj šíri po kvantách (1905);

· pri interakcii svetla s hmotou fotóny odovzdávajú energiu E_n = nhf , kde n = 1,2,3,.... (1905);

· pri interakcii svetla s hmotou fotóny odovzdávajú i  hybnosť po diskrétnych kvantách (1916).

Veľkosť hybnosti fotónu p spojeného so svetelnou vlnou o frekvencii f je určená vzťahom

Tento vzťah vyplýva z teórie relativity a možno ho odvodiť z relativistického vzťahu pre energiu častice s pokojovou hmotnosťou m_{o ,} keď postulujeme fotón ako časticu s nulovou pokojovou hmotnosťou , t.j. m₀ = 0.

V roku 1921 Arthur Compton svojim pokusom, ktorý podľa neho nesie i názov - Comptonov jav, experimentálne dokázal Einsteinovu myšlienku o kvantovaní energie a hybnosti svetla, odovzdávanú prostredníctvom fotónov pri zrážke fotónu s elektrónom.

Compton študoval chovanie sa fotónov s rovnakou energiou pri prechode fóliami z rôznych látok. Vo svojom experimente nechal dopadať zväzok röntgenových lúčov s vlnovou dĺžkou l = 71,1 pm na uhlíkový terč a skúmal intenzitu rozptýlených röntgenových lúčov terčom do  priestoru. Závislosť intenzity rozptýleného fotónu od vlnovej dĺžky pre štyri rozptylové uhly j (j = 0 ⁰, 45 ⁰, 90 ⁰, 135 ⁰), ukazuje obr. 13.1.4.1.

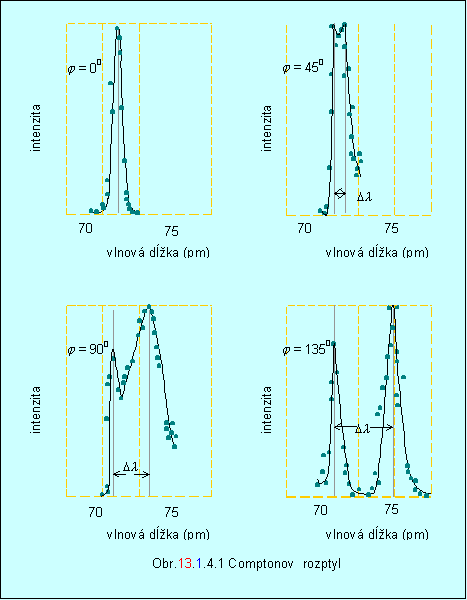
Z experimentálnych meraní Compton zistil nasledovné skutočnosti:

· pri rozptyle bolo pozorované žiarenie odpovedajúce vlnovej dĺžke dopadajúcemu fotónu l a tiež žiarenie s väčšou vlnovou dĺžkou l´;

· zmena vlnovej dĺžky Dl nezávisí od vlnovej dĺžky l dopadajúceho fotónu, ale závisí od uhlu rozptylu j. So zväčšovaním uhla j sa zväčšuje rozdiel Dl;

· so zväčšovaním uhla rozptylu intenzita pôvodného žiarenia klesá a zvyšuje sa intenzita rozptýleného žiarenia;

· maximálna zmena vlnovej dĺžky D l nastane pri uhle rozptylu j = 180 ^o a je rovná dvojnásobku Comptonovej vlnovej dĺžky l_C.

Uvedené experimentálne merania Arthur Compton matematicky popísal na základe skúmania zrážky fotónu röntgenového žiarenia s niektorým elektrónom z obalu atómu uhlíka. Proces zrážky fotónu s elektrónom skúmal ako pružnú zrážku dvoch biliardových gúľ v klasickej mechanike, v dôsledku ktorej dochádza k zmene vlnovej dĺžky rozptýleného fotónu.

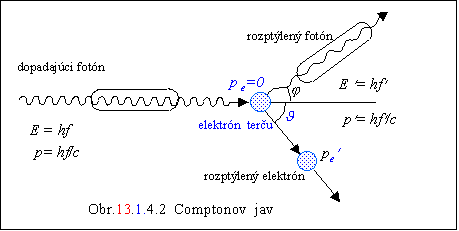
Proces zrážky znázorňuje obr. 13.1.4.2 - fotón s energiou hf a hybnosťou p = hf / c dopadne na elektrón (o ktorom predpokladáme, že je nehybný v laboratórnej sústave), rozptylom sa odchyľuje od svojho pôvodného smeru o uhol j a stráca energiu, zatiaľ čo elektrón získa impulz a začne sa pohybovať v smere určenom uhlom J.

To znamená, že fotón stráca v procese zrážky také množstvo energie, ktoré sa rovná kinetickej energii E_k získanej pri zrážke s elektrónom. Ak frekvencia dopadajúceho fotónu je f ( resp. vlnová dĺžka l), má rozptýlený fotón nižšiu frekvenciu f ´ (resp. väčšiu vlnovú dĺžku l´ ). Z platnosti zákona zachovania energie a zákona zachovania hybnosti pre izolovaný systém fotón - elektrón Arthur Compton odvodil všeobecný vzťah, ktorý udáva zmenu vlnovej dĺžky fotónu pri rozptyle o uhol j na častici s pokojovou hmotnosťou m_o daný rovnicou

Konštantná veličina h/m_oc sa nazýva Comptonova vlnová dĺžka l_C rozptyľujúcej častice. Z rovnice (13.1.4.2) vidieť, že najväčšia zmena vlnovej dĺžky nastane pre uhol j = 180 ^o . V tomto prípade D l = 2 l_C . Pretože l_C pre elektrón je rovná 2,4 .10^-12 m, maximálna zmena vlnovej dĺžky pri Comptonovom jave je 4,8. 10^-12 m . Pre ostatné častice je totiž Comptonova vlnová dĺžka podstatne menšia, nakoľko ich pokojová hmotnosť m₀ je väčšia. Ak využijeme znalosť trigonometrických funkcií, možno ukázať, že pre zmenu vlnovej dĺžky fotónu pri rozptyle platí vzťah v tvare:

(13.1.4.3)

Comptonov vzťah je jedným z dôkazov korpuskulárnej povahy svetla, ktorý skúma zrážku medzi dopadajúcim fotónom a časticou, napr. elektrónom.

–––––––––––––––––––––––––––––––––––––––––––––––––

Príklad 13.1.4.1 Za predpokladu, že elektrón je v pokoji ukážte, že pre zmenu vlnovej dĺžky pri dopade fotónu na elektrón platí Comptonov vzťah:

,

kde l je vlnová dĺžka fotónu pred dopadom na elektrón a l´ je vlnová dĺžka po rozptyle na elektróne, j je uhol, o ktorý sa fotón rozptýli vzhľadom na svoj pôvodný smer pohybu, m₀ je pokojová hmotnosť elektrónu a h je Planckova konštanta!

Riešenie: Na interakciu elektrónu s fotónom (obr. 13.1.4.1) možno pozerať ako na zrážku dvoch pružných gúľ, pri ktorej platí zákon zachovania energie a zákon zachovania hybnosti. Fotón stráca v procese zrážky také množstvo energie, ktoré sa rovná kinetickej energii E_k získanej pri zrážke elektrónom. Ak frekvencia dopadajúceho fotónu je f ( resp. vlnová dĺžka l), má rozptýlený fotón nižšiu frekvenciu f ´ (resp. väčšiu vlnovú dĺžku l´), takže platí l < l´ a f > f´´. Z týchto dvoch zákonov sformulujeme dve rovnice, jednu skalárnu a druhú vektorovú. Matematická formulácia zákona zachovania energie je:

, (1)

resp. pomocou energie fotónov

. (2)

Nakoľko fotón je postulovaný ako častica s nulovou pokojovou hmotnosťou možno celkovú energiu fotónu vyjadriť ako

. (3)

Označme p_e počiatočnú a  p_e´ konečnú hybnosť elektrónu , pričom platí p_e = 0 a počiatočnú a konečnú hybnosť fotónu ako p a p´. Zo zákona zachovania hybnosti platí:

Matematická formulácia zákona zachovania hybnosti je:

(4)

Na rozdiel od energie, hybnosť je vektorová veličina a musí sa zachovávať v každom z dvoch navzájom kolmých smerov. Nech fotón dopadá na nehybný elektrón v kladnom smere osi x. Druhým uvažovaným smerom nech je smer kolmý na pohyb fotónu, ležiaci v rovine určenej rozptýleným fotónom a elektrónom. Pre nehybný elektrón platí p_e = 0 a pre veľkosť počiatočnej a konečnej hybnosti fotónu

. (5)

Zákon zachovania hybnosti z vektorového tvaru (5) prepíšme do dvoch skalárnych rovníc pre zvolené dva smery x, y. .V smere osi x platí:

. (6)

V smere osi y platí:

, (7)

kde sme využili skutočnosť, že platí. p^¢ sin(2p-J )=p^¢ sinJ. Nakoľko uhol odklonu elektrónu po zrážke J nepoznáme (a z experimentálnych meraní ho ani nebolo možné určiť), umocnením upravených rovníc (6) a (7) na druhú a ich sčítaním, neznámy uhol J z rovníc vylúčime:

. (8)

Ak porovnáme dva vzťahy pre celkovú energiu častice

, (9)

, (10)

získame rovnicu

, (11)

resp. po umocnení

, (12)

odkiaľ pre elektrón

. (13)

Porovnaním rovníc (8) a (13) dostávame

. (14)

Po dosadení vzťahu (2) za kinetickú energiu elektrónu platí

,

, (15)

čo je vzťah, ktorý sme mali odvodiť. Ak ešte použijeme rovnicu

,

Comptonov vzťah (15) možno upraviť na tvar

–––––––––––––––––––––––––––––––––––––––––––––––

Príklad 13.1.4.2 Vysvetlite prečo v spektre rozptýleného fotónu pri Comptonovom jave sa vyskytuje i podstatná zložka s pôvodnou vlnovou dĺžkou dopadajúceho žiarenia .

Riešenie: Pri odvodzovaní vzťahu pre zmenu vlnovej dĺžky fotónu pri rozptyle o uhol j na častici s pokojovou hmotnosťou m_o daného rovnicou (13.1.4.2) Compton predpokladal, že rozptyľujúca častica je celkom voľná a môže sa pohybovať celkom ľubovolne. Tento predpoklad bolo možné využiť, nakoľko mnohé elektróny v látke sú len slabo viazané k svojim atómom. Niektoré elektróny sú však v atóme silne viazané a tak pri zrážke s fotónom odskakuje namiesto jedného elektrónu celý atóm. V tomto prípade za hodnotu m_o do vzťahu (1) treba dosadiť pokojovú hmotnosť celého atómu, ktorá je však väčšinou rádove desaťtisíckrát väčšia ako pokojová hmotnosť elektrónu. Z tohto dôvodu Dl je veľmi malá a nie sme ju schopní zaregistrovať.

V spektrálnom rozložení intenzity pri rozptyle na pevne viazanom elektróne sa vlnová dĺžka rozptýleného fotónu neodlišuje od pôvodnej vlnovej dĺžky, preto v rozptýlenom žiarení možno pozorovať súčasne s posunutou čiarou i maximum odpovedajúce dopadajúcej vlnovej dĺžke fotónu l.

––––––––––––––––––––––––––––––––––––––––––-

Príklad 13.1.4.3 Vypočítajte percentuálnu zmenu vlnovej dĺžky rozptýleného fotónu s vlnovou dĺžkou a) 550 nm b) 10^-10 m pri rozptyle o 180 ^o na elektróne, ktorý predpokladáme, že sa nachádza v pokoji. Pokojovú hmotnosť elektrónu je 9,1 .10^-31 kg. Rozhodnite, ktorý z dvoch udaných zdrojov žiarenia by ste použili na vyšetrovanie Comptonovho javu a zdôvodnite prečo.

Riešenie: Pre zmenu vlnovej dĺžky fotónu pri rozptyle o uhol j na častici s pokojovou hmotnosťou m_o platí

rovnica (13.1.4.3) . Percentuálnu zmenu vlnovej dĺžky určíme zo vzťahu

.

Po dosadení číselných hodnôt dostávame v prípade a):

.

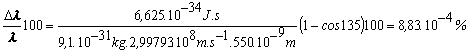V prípade b) Dl / l = 4,8568 %. Na skúmanie Comptonovho javu použijeme röntgenove žiarenie, nakoľko percentuálna zmena Dl je niekoľko percent, kým pri viditeľnom žiarení je Dl len niekoľko desaťtisícin %. Z tohto dôvodu experimenty Compton uskutočňoval s röntgenovým žiarením.

––––––––––––––––––––––––––––––-

Kontrolné otázky

1. Vysvetlite, v čom spočíva Comptonov experiment.

2. Z akých zákonov vychádzame pri odvodení vzťahu pre Comptonov jav.

3. Formulujte matematicky základné zákony pre Comptonov jav.

4. Ak viete, že hmotnosť protónu je 1863 -násobok hmotnosti elektrónu, zdôvodnite na ktorej častici je Comptonov rozptyl väčší.

5. Definujte Comptonovu vlnovú dĺžku.

6. Je vlnová dĺžka rozptýleného fotónu väčšia alebo menšia ako vlnová dĺžka dopadajúceho fotónu?

7. Závisí Comptonov vzťah od uhlu odklonu elektrónu od pôvodného smeru fotónu?

8. Kedy sa rovná pozorovaná zmena vlnovej dĺžky dvojnásobku Comptonovej vlnovej dĺžky?