8.4            Kapacita, Energia elektrostatického poľa

 

Elektrostatické pole má svoju materiálnu povahu. Prejavuje sa tým, že samotné pole má elektrickú energiu a tá sa rozprestiera všade tam, kde je pole nenulovej intenzity. Podstatu tejto skutočnosti si vysvetlíme najprv vysvetlením pojmu energia nabitého telesa. K tomu

 

Potrebné vedomosti

Pochopenie tejto kapitoly, vyžaduje poznať pojmy z elektrostatiky, ako je elektrický náboj, Coulombova sila, práca elektrických síl, intenzita elektrického poľa, potenciál. Poznať vlastnosti vodiča v elektrickom poli.

 

Učebné ciele

Študent má vedieť definovať pojmy kapacita osamelého vodiča, kondenzátora. Má vedieť odvodiť súvis energie a práce v elektrickom poli a vyjadriť energiu sústavy nábojov, nabitého telesa.

Má vedieť vysvetliť pojem hustota elektrickej energie, tak aby sa tento pojem dal uplatniť aj pre pole elektromagnetické a pre šírenie energie takéhoto poľa vo forme vlnenia.

 

Kľúčové slová

kapacita osamelého vodiča, kapacita kondenzátora, elektrická energia, energia elektrického poľa energia  sústavy nábojov, hustota elektrickej energie

 

8.4.1        Kapacita osamelého vodiča a kondenzátora.

 

Potenciál poľa v okolí bodového náboja je úmerný veľkosti náboja. Podobne je potenciál nabitého vodiča úmerný náboju na jeho povrchu. Pomer celkového náboja Q vodiča k jeho potenciálu V na povrchu vodiča (všade na povrchu aj vo vnútri vodiča je rovnaký) sa nazýva  kapacita vodiča

                                                                                                                                                                                                                  (8.4.1.1)

Kapacita, aj keď je definovaná pomocou náboja na vodiči, ako uvidíme nezávisí od tohto náboja, je funkciou len tvaru vodiča. Napr. vypočítajme kapacitu osamelej gule: ak ju nabijeme nábojom Q, potom jej potenciál a kapacita je

                                                                                                                                                                          (8.4.1.2)

Čím je kapacita väčšia, tým väčším nábojom je možné vodič nabiť, pričom potenciál neprestúpi prípustnú hodnotu (napr. hodnotu, pri ktorej sa náboj začne strhávať do ovzdušia). Jednotkou kapacity je farad (F), pričom podľa definície kapacity preň platí

Je to veľmi veľká jednotka, v praxi sa používajú menšie. Kapacitu 1 mF by mala osamelá guľa s polomerom 9 km.

Uvedené skutočnosti platia len pre osamelý vodič, pre ktorý rozloženie náboja na ňom nie je ovplyvnené inými vonkajšími poliami. V opačnom prípade podľa princípu superpozície výsledný potenciál na povrchu nabitého vodiča závisí aj od okolitých nabitých vodičov, ktoré vytvárajú pole s nejakým potenciálom aj v mieste prvého vodiča. Tento potenciál sa algebraicky pripočíta k potenciálu prvého vodiča. Prítomnosťou okolitých nabitých vodičov sa náboj na prvom vodiči nezmení, zmení sa ale výsledný potenciál na jeho povrchu a tým sa zmení aj jeho kapacita. Treba si uvedomiť že pokiaľ okolité vodiče majú náboj s opačným znamienkom ako vodič, kapacitu ktorého určujeme, aj potenciály ich polí budú mať opačné znamienko a od potenciálu prvého vodiča sa odpočítajú. Vo vzťahu  (8.4.1.1) pre výpočet kapacity sa náboj nezmení, potenciál v menovateli sa zmenší a tým sa zväčší kapacita vodiča. Veľkého účinku sa dá dosiahnuť  tesným priblížením druhého vodiča s opačným, rovnako veľkým nábojom. Tento druhý vodič sa zároveň môže voliť tak, aby odtienil prvý vodič od vplyvu ďalších nabitých telies. Takéto zoskupenie dvoch vodičov sa nazýva kondenzátor. Ak sa jeden vodič kondenzátora nabije nábojomQ+, druhý sa obvykle uzemní, takže sa na ňom indukuje rovnako veľký opačný náboj  Q-. Kapacita kondenzátora je potom podiel náboja na prvom vodiči a rozdielu potenciálov prvého a druhého vodiča t.j. napätia medzi prvým a druhým vodičom U

                                                                                                                                                                                      (8.4.1.3)

 

8.4.2        Kapacita doskového kondenzátora.

 

Doskový kondenzátor sa skladá z dvoch kovových platní oddelených tenkou vrstvou dielektrika. Dosky nabijeme rovnako veľkými opačnými nábojmi. Tieto sa rozložia po ich povrchu zhruba rovnomerne s hustotami +s a -s. Ak je hrúbka dielektrika oveľa menšia ako rozmery dosiek, môžeme tieto považovať za nekonečne veľké a v zhode s časťou (8.1.9.1) pole medzi nimi za homogénne s intenzitou

kolmou na povrch dosiek. Napätie medzi doskami je

.
Ak plošný obsah každej z dosiek je S, potom náboj na kladnej doske je  Q =sS.

Po dosadení do (8.4.1.1) je kapacita daná vzťahom

.                                                                                                                                                                                                                 (8.4.2.1)

Kapacita doskového kondenzátora je úmerná plošnému obsahu dosiek a nepriamo úmerná vzájomnej vzdialenosti dosiek.

 

8.4.3        Energia sústavy nábojov

 

Jednoduchými pokusmi sa môžeme presvedčiť, že elektrostatické pole má svoju energiu, ktorá vyjadruje schopnosť konať prácu na úkor zmeny tohoto poľa. Ak dosky nabitého kondenzátora spojíme vodičom, potom elektrický prúd vyvinie na vodiči teplo, ktorého veľkosť priamo súvisí so zmenou napätia na kondenzátore.

Úbytok energie elektrického poľa preto môžeme vyjadriť pomocou práce, ktorú toto pole vykoná. Opačne veľkosť energie poľa sa dá vypočítať ako práca vonkajších síl, ktoré dané pole premiestnením náboja vytvoria.

V časti 8.1.9 sme vyjadrili prácu pri premiestňovaní náboja v elektrickom poli. Energia náboja Q v danom mieste elektrického poľa sa rovná sa práci, ktorú musia vykonať vonkajšie sily pri premiestnení náboja do daného miesta zo zvoleného vzťažného bodu. Vzťažný bod sme volili v nekonečne, kde sila elektrického poľa je nulová. Vytvorme elektrické pole E2 bodovým nábojom Q2 a premiestňujme v jeho poli náboj Q1 do bodu 1.  Potom táto práca sa dá vyjadriť:

 ,                                                                                                                                                                                       (8.4.3.2)

kde vonkajšia sila je opačná k elektrickej sile Q1E2, a V1 je potenciál elektrického poľa vytvorený nábojom Q2 v bode 1.

Celú situáciu môžeme vytvoriť i opačným postupom. Do poľa vytvoreného nábojom Q1 vkladajme náboj Q2 do miesta 2, tak že postavenie nábojov bude rovnaké, potom aj práca bude rovnaká o čom sa môžeme presvedčiť zo vzťahu pre potenciál bodového náboja .Takže môžeme napísať elektrostatickú energiu dvoch bodových nábojov i v symetrickej forme:

 ,              

Posledný vzťah sa dá i zovšeobecniť pre sústavu bodových nábojov. Energia elektrického poľa sústavy nábojov je daná vzťahom:

,                                                                                                                                                                                                      (8.4.3.3)

kde Vi , je potenciál (vzhľadom na nekonečno) sústavy všetkých nábojov okrem náboja Qi .

.

8.4.4        Energia elektrostatického poľa nabitého vodiča

 

Majme kondenzátor kapacity C nabitý nábojom Q na napätie U. Ako bolo ukázané v časti 8.1.10, elektrostatické pole je schopné konať prácu pri premiestňovaní náboja . Pokiaľ by náboj v kondenzátore mohol prechádzať z jednej dosky na druhú, elektróny by boli poľom urýchlené, získali by kinetickú energiu (pokiaľ by sa táto nepremenila odporom vedenia na teplo), kondenzátor by sa vybil, pole medzi doskami by vymizlo. V súlade so zákonom zachovania energie musí mať elektrostatické pole energiu W, ktorá sa pri vybíjaní kondenzátora premení na inú formu. Je zrejmé, že táto energia sa musí rovnať práci na nabitie pôvodne nenabitého kondenzátora, to znamená na postupné prenesenie kladného náboja z dosky zápornej na kladnú. Na prenesenie prvého elementárneho kladného náboja dQ+ nie je potrebná práca, tento však vytvorí medzi doskami kondenzátora elektrostatické pole. Pri prenášaní ďalšieho náboja  dQ+ už proti pohybu pôsobí sila elektrostatického poľa. Ak je kondenzátor už nabitý nábojom dQ+ na napätie U, je na prenesenie náboja  dQ+  potrebná práca

.
Celá práca potrebná na nabitie pôvodne nenabitého kondenzátora, to znamená na postupné prenesenie  celého náboja Q na kladnú dosku, je

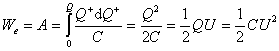.                                                                                                                                                         (8.4.4.1)

Podobný vzťah by sme dostali aj v prípade, že by sme nabíjali osamelý vodič, prenášaním náboja z veľkej vzdialenosti na vodič. V tom prípade napätie U je v skutočnosti konečný potenciál V , ktorý by mal vodič po nabití nábojom Q:

                                                                                                                                                                                                             (8.4.4.2)

Tento vzťah je zhodný zo vzťahom (8.4.3.3) pre sústavu nábojov, všetky čiastkové náboje sú na potenciáli vodiča V a ich súčet je Q.

 

 

8.4.5        Hustota energie elektrického poľa

 

Počítajme energiu nabitého doskového kondenzátora. Predpokladajme, že rozmery dosiek sú veľké v porovnaní so vzdialenosťou dosiek, medzi doskami je dielektrikum permitivity e. Potom môžeme predpokladať, že pole medzi doskami je homogénne a je vytvorené len v objeme t medzi doskami kondenzátora. Za predpokladu homogénneho poľa je

,

kde E je intenzita tohoto poľa a d vzdialenosť dosiek kondenzátora.  Kapacita doskového kondenzátora je daná vzťahom (8.4.2.1), kde S je obsah plochy dosky.  Potom po dosadení do vzťahu (8.4.4.1) dostávame a s ohľadom na (8.3.5.1)

,

kde  je objem homogénneho poľa v kondenzátore. Energiu pripadajúcu na jednotku objemu nazveme hustotou energie elektrostatického poľa we

.                                                                                                                                                                                                            (8.4.5.1)

Tento vzťah sa dá zovšeobecniť aj pre pole nehomogénne. Ako bolo povedané v časti (8.3.6) v anizotropnom dielektriku nemá  vektor elektrostatickej indukcie rovnaký smer ako vektor intenzity elektrostatického poľa. V takýchto poliach platí všeobecnejší vzťah

.                                                                                                                                                                                                         (8.4.5.2)

Energia elektrostatického poľa je skutočne rozložená v priestore, kde sa nachádza pole, toto pole je schopné konať prácu, urýchľovať v ňom sa nachádzajúce nabité častice. U premenného elektromagnetického poľa ako je napr. svetlo nám vôbec nenapadne jeho energiu spájať s nejakým nábojom, ktorý ho vytvoril.

 

 

Príklad 8.4.1 Tri vodivé rovinné rovnaké dosky sú uložené paralelne vo vzdialenostiach d . Vypočítajte kapacitu kondenzátora, ktorý vytvoríme spojením krajných dosiek, druhou doskou kondenzátora je stredová doska

Riešenie

 

Príklad 8.4.2 Vypočítajte kapacitu paralelne zapojených kondenzátorov a aplikujte tento výsledok na prípad rovinného doskového kondenzátora s plošným obsahom dosiek S  =100 cm2 , ktorých vzdialenosť je d = 2 mm, ak zvislé dosky sú ponorené do etylalkoholu s relatívnou permitivitou  er= 26 do jednej tretiny svojej plochy.

Riešenie

 

Príklad 8.4.3 Urobte odhad „polomeru“ elektrónu za predpokladu, že je to guľa a jej pokojová energia E = mc2, (kde hmotnosť elektrónu m = 9 . 10-31 kg, rýchlosť svetla c = 3 . 108 m. s-1 ) je rovná energii vytvoreného elektrického poľa!

Riešenie

 

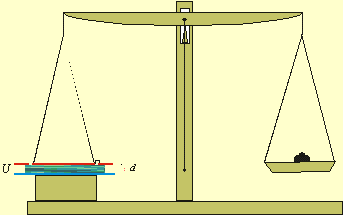
Obr. 8.4.1

Kirchoffove váhy

 

Príklad 8.4.4 Pomocou Kirchhoffových váh vyjadrite permitivitu kvapalného prostredia vloženého medzi dosky kondenzátora týchto váh! Kirchhoffove váhy tvorí kondenzátor umiestnený na váhy tak, že umožňuje merať elektrickú silu, ktorou je priťahovaná pohyblivá doska kondenzátora, ak tento je nabitý na napätie U. Usporiadanie váh podľa obr.(8.4.1) (zavesená pohyblivá kruhová doska plošného obsahu S je spojená vodivo s obkolesujúcim medzikružím) umožňuje predpokladať, že elektrické pole v kondenzátore je homogénne. Vzdialenosť pohyblivej dosky od druhej pevnej dosky je d.

Riešenie

 

 

 

 

 

 

 

 

Kontrolné otázky