Coulombova veta - odvodenie

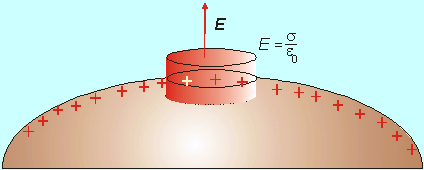
Doteraz sme popisovali elektrické pole v nenabitých vodičoch vo vonkajších elektrických poliach. Rovnaké vlastnosti bude mať aj elektrické pole, ktoré je vytvorené nabitým vodičom. Nech na vodivom telese je náboj Q. Tento sa rozloží v telese tak, že pole vo vnútri vodiča je nulové. Preto aj náboj je rozložený len na ploche povrchu vodivého telesa. Elektrické pole na povrchu vodiča smeruje kolmo na povrch vodiča v danom mieste. Jeho veľkosť určuje tzv. Coulombova veta, ktorú odvodíme z Gaussovej vety. Zvoľme si uzatvorenú plochu, ktorú tvorí povrch malého valčeka.

Obr. 8.2.3.2

Odvodenie Coulombovej vety

Tento umiestnime do skúmaného poľa tak, že jednou podstavou leží vo vodivom telese a druhá je nad vodičom (Obr.8.2.3.2). Jeho výšku voľme veľmi malú, plochu podstavy takú malú, aby v každom jej bode intenzita poľa bola rovnaká. Potom tok intenzity elektrického poľa je nenulový len cez podstavu z vonkajšej strany telesa (vo vnútri je intenzita nulová, na stene vektor intenzity leží v ploche steny preto E . dS = 0):

(8.2.3.3)

Náboj uzatvorený v objeme valčeka je náboj rozložený na povrchu časti plochy telesa:

(8.2.3.4)

Po dosadení do Gaussovej vety z rovníc (8.2.3.3 a 4) intenzita na povrchu vodiča v mieste s plošnou hustotou náboja s je

(8.2.3.5)

Coulombova veta: Elektrická intenzita nad povrchom vodiča je kolmá na povrch vodiča a úmerná plošnej hustote náboja. Konštanta úmernosti je prevrátená hodnota elektrickej konštanty (permitivity vákua).

Poznámka:

V časti 8.1.9.1, vzťah (8.1.9.1.5) bolo odvodené, že elektrická intenzita nad povrchom nekonečnej rovinnej dosky, nabitej s plošnou hustotou s je polovičná, treba to chápať tak, že aj náboj z každej "strany" roviny "na povrchu" je len polovičný.