1.2 Súčiny medzi vektormi

Vektorová algebra popri násobení vektorov skalármi zavádza aj súčiny medzi vektormi.

Skalárny súčin dvoch vektorov je zavedený ako operácia, ktorej výsledkom je skalárna veličina. Hodnota tejto skalárnej veličiny je určená súčinom veľkostí príslušných vektorov a kosínusu uhla, ktorý tieto vektory zvierajú. Fyzikálny rozmer výslednej skalárnej veličiny sa rovná súčinu rozmerov násobených vektorových veličín. Skalárny súčin sa označuje bodkou medzi vektormi, v strede výšky písmen (nie na úrovni riadku) :

a × b = ab cos a . (1.2.1)

Pritom uhol medzi dvoma vektormi sa určuje tak, aby nebol väčší ako p radiánov (180 o). Bezpečne ho určíme tak, keď oba vektory nakreslíme so spoločným začiatkom.

Niektoré vlastnosti skalárneho súčinu

a × b = b × a (1.2.2)

i × i = 1 , j × j = 1 , k × k = 1 , i × j = 0 , i × k = 0, j × k = 0 (1.2.3)

a × (b + c) = a × b + a × c(1.2.4)

alebo všeobecnejšie :

(a1 + a2 + … + ap) × (b1 + b2 + …+ bq) = a1 × b1 + a1 × b2 +…+ a1× bq + … + ap × bq

a × b = (ax i + ay j + az k) × (bx i + by j + bz k ) = ax bx + ay by + az bz , (1.2.5)

napríklad (3 i + 2 j - k) ×  (- i + 2 j - 2 k ) = - 3 + 4 + 2 = 3 .

, (1.2.6)

takže porovnaním (1.2.5) a (1.2.6) môžeme získať vzorec na výpočet (kosínusu) uhla medzi vektormi :

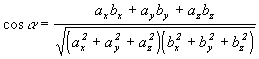
(1.2.7)

ax = a × i , ay = a × j , az = a × k (1.2.8)

s = ax i = (a × i) i , t = ay j = (a × j) j , u = az k = (a × k) k (1.2.9)

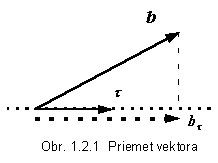
Tento postup môže poslúžiť aj pri vytváraní ortogonálneho priemetu vektora do ľubovoľného smeru v priestore, určeného jednotkovým vektorom. Napríklad priemet bt (na obr. 1.2.1 čiarkovaný) vektora b do smeru jednotkového vektora t získame tak, že vypočítame ich skalárny súčin a takto získaným skalárom vynásobíme vektor t :

bt = (b × t )t (1.2.10)

Skalárny súčin sa často využiva v mechanike, a teórii elektromagnetického poľa. Napríklad skalárnym súčinom vektora sily f a vektora elementárneho posunutia dr sa vyjadruje elementárna práca dW = f × dr = f dr cos a , lebo smer sily a smer posunutia telesa nemusia byť rovnaké. Vtedy sa na vykonanie práce využíva iba priemet sily do smeru posunutia, vyjadrený ako f cosa .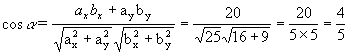

Príklad 1.2.1 Na obr.1.2.2 je znázornený trojuholník určený vektormi a = 5i , b = 4i + 3j . Vypočítajte uhly medzi stranami a , b a stranami a, c .

 

 

čiže a = 36,9o . Na výpočet uhla b potrebujeme vyjadriť vektor c = b - a = - i + 3j a opäť použiť vzorec (1.2.7). Musíme si však uvedomiť, že 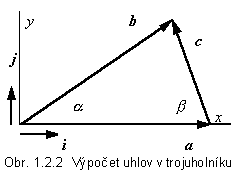vektor a s vektorom c zviera uhol g = 180o - b . Tak dostaneme :

cos g = - 1/ , čiže g = 108,43 o .

 

 

 

 

Vektorový súčin dvoch vektorov je operácia, ktorej výsledkom je vektor. Preto treba definovať nie iba veľkosť výsledku, ale aj smer výsledného vektora. Vektorový súčin sa označuje krížikom medzi vektormi :

c = a ´ b(1.2.11)

Veľkosť c výsledného vektora c je definovaná ako súčin veľkostí násobených vektorov a sínusu uhla nimi zovretého :

c = ab sina (1.2.12)

Pre smer vektora c platí definícia, že je kolmý na rovinu násobených vektorov. Jednoznačnosť definície však vyžaduje určiť, na ktorú stranu roviny smeruje. Vektor c má taký smer, že z jeho konca sa stotožnenie prvého vektora zo súčinu (v tomto prípade vektora a) s druhým vektorom po kratšom oblúku javí ako pohyb proti chodu hodinových ručičiek. O trojici vektorov a, b, c v danom poradí potom hovoríme, že tvoria pravotočivú sústavu vektorov. Zmena ich poradia jednou permutáciou znamená zmenu z pravotočivej na ľavotočivú sústavu (trojicu).

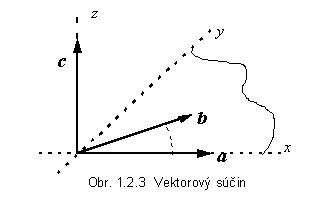
Na obr. 1.2.3 je trojica vektorov a, b, c znázornená v axonometrickom pohľade. Pre názornosť sú nakreslené aj súradnicové osi karteziánskej sústavy. Ak otáčanie vektora a k vektoru b po kratšom oblúku napodobíme otáčaním pravotočivej skrutky, umiestnenej v začiatku súradnicovej sústavy kolmo na rovinu vektorov a b , skrutka sa bude posúvať v smere vektora c . Aj tento model pomáha pri určovaní smeru vektora, ktorý je výsledkom vektorového súčinu .

Niektoré vlastnosti vektorového súčinu

  • Vektorový súčin nie je komutatívna operácia, lebo zámena poradia vektorov poskytuje síce vektor rovnako veľký, ale opačného smeru. Táto skutočnosť sa zapisuje v tvare :

a ´ b = - b ´ a(1.2.13)
  • Veľkosť vektorového súčinu dvoch vektorov možno interpretovať ako plošný obsah rovnobežníka vytvoreného týmito vektormi. Navyše výsledný vektor jednoznačne určuje orientáciu roviny v priestore, preto ho možno chápať ako vektor priradený ploche.
  • Z definície veľkosti vektorového súčinu vyplýva, že vektorový súčin dvoch kolineárnych vektorov sa rovná nule (je nulový vektor).
  • Pre jednotkové vektory i , j , k  , ktoré sú navzájom na seba kolmé, platia vzťahy :

i ´ i = 0 j ´ j = 0 k ´ k = 0 (1.2.14)

i ´ j = k  j ´ k = i k ´ i = j j ´ i = - k k ´ j = - i i ´ k = - j

  • Pre vektorový súčin platí distributívny zákon :

a ´ (b + c) = a ´ b + a ´ c (b + c) ´ a = b ´ a + c ´ a (1.2.15)

Dva prípady distributívneho zákona sú uvedené preto, lebo vo vektorovom súčine nemožno zamieňať poradie vektorov bez zmeny znamienka.

  • Na základe distributívneho zákona vektorový súčin vektorov vyjadrených v zložkovom tvare môžeme vyjadriť nasledovne :

a ´ b = (ax i + ay j + az k) ´ (bx i + by j + bz k ) =

= axbx(i ´ i) + axby(i ´ j) + axbz(i ´ k) +

+ aybx(j ´ i) + ayby(j ´ j) + aybz( j ´ k) +

+ azbx(k ´ i) + azby(k ´ j) + az bz(k ´ k) =

= 0 + axby k - axbz j +

- aybx k + 0 + aybz i +

+ azbx j - azby i + 0 =

= i (aybz - azby ) + j (azbx - axbz ) + k (axby - aybx ) (1.2.16)

Čitateľovi, ktorý pozná determinanty je zrejmé, že posledný výraz možno formálne vyjadriť ako determinant :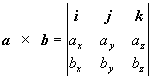

(1.2.17)

ho = h / 7 = (3/7) i + (2/7) j + (6/7) k .

S vektorovým súčinom sa stretneme napríklad pri vyjadrení momentu sily M = r ´ f, kde r je polohový vektor pôsobiska sily f , alebo pri vzťahu pre silu f pôsobiacu na elektrický náboj q pohybujúci sa v magnetickom poli s magnetickou indukciou B : f = qv ´ B .

Príklad 1.2.4 Vypočítajte skalárny násobok vektorového súčinu vektorov a = 5 i , b = 4 i + 3 j z príkladu (1.2.2) skalárom p = 2 .

Riešenie : pc = p(a ´ b ) = p[ (5i) ´ (4 i + 3 j)] = p (15 k) = 30 k .

Poznámka : Rovnaký výsledok dostaneme, ak skalárom p vynásobíme niektorý z vektorov a, b ešte pred uskutočnením vektorového súčinu :

a) pc = p(a ´ b ) = (pa ´ b) = (10 i) ´ (4 i + 3 j) = 30 k

b) pc = p(a ´ b ) = (a ´ pb) = (5 i) ´ (8 i + 6 j) = 30 k

Z výsledku vyplýva významné pravidlo, že nezáleží na tom, ktorému z vektorov vektorového súčinu priradíme skalár, ktorým vektorový súčin násobíme.

Zmiešaný súčin troch vektorov je operácia, v ktorej sa uskutoční najprv vektorový a po ňom skalárny súčin. Medzi tromi vektormi a, b, c je možných viacero variantov zmiešaného súčinu, napríklad :

a × (b ´ c), (a ´ b) × c , (b ´ c) × a (1.2.18)

Výsledkom je vždy skalárna veličina, ktorá môže byť kladná, nulová i záporná.

 

Niektoré vlastnosti zmiešaného súčinu .

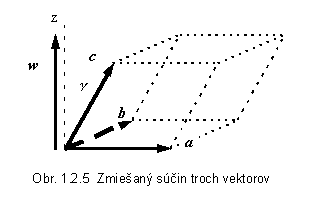
  • Výraz (a × b) ´ c , nie je zmiešaný súčin, lebo výraz v zátvorke je skalárna veličina, ktorou nemožno vektor c násobiť vektorovo.
  • Zmiešaný súčin má význam objemu rovnobežnostena skonštruovaného na základe vektorov zmiešaného súčinu. Na obrázku 1.2.5 je nakreslený rovnobežnosten zostrojený pomocou vektorova, b, c , ako aj priamka z   kolmá na rovinu vektorov a, b . Zmiešaný súčin

S = (a ´ b) × c vypočítame podľa pravidiel vektorového a skalárneho súčinu . Výsledkom vektorového súčinu a ´ b je vektor (označme ho w) kolmý na ich rovinu, teda vektor, ktorý má veľkosť ab sina a je rovnobežný s priamkou z . Vektor w zviera s vektorom c uhol g , ktorého kosínus vstupuje do výrazu pre skalárny súčin medzi vektormi w a c . Pre výsledok zmiešaného súčinu tak dostaneme S = (ab sina ) c cosg . Výraz c cosg súčasne predstavuje výšku rovnobežostena, pričom veľkosť vektorového súčinu ab sina je plošný obsah jeho základne. Preto zmiešaný súčin má význam objemu rovnobežnostena.

  • Objem toho istého rovnobežnostena dostaneme aj pomocou zmiešaných súčinov (b ´ c) × a a (c ´ a) × b , teda súčinmi, v ktorých sme urobili cyklickú zámenu poradia vektorov, pri zachovaní polohy zátvoriek, ako aj značiek vektorového a skalárneho súčinu. Preto platia rovnosti

(a ´ b) × c = (b ´ c) × a = (c ´ a) × b (1.2.19)

  • Ak si uvedomíme komutatívnosť skalárneho súčinu, môžeme napísať rovnosť

(a ´ b) × c = c × (a ´ b ) (1.2.20) Porovnaním posledných členov  rovností (1.2.19) a (1.2.20) dostaneme výsledok

(c ´ a) × b = c × (a ´ b ) (1.2.21)

ktorý interpretujeme ako možnosť premiestnenia zátvoriek, pri súčasnej výmene značiek vektorového a skalárneho súčinu.

  • Zmiešaný súčin je kladný, ak vektory v zmiešanom súčine, v takom poradí ako sú napísané, tvoria pravotočivú sústavu. Zámenou poradia ľubovoľných dvoch vektorov v zmiešanom súčine, zmení sa jeho znamienko. Ak je zmiešaný súčin záporný, objemu rovnobežnostena sa vtedy rovná jeho absolútna hodnota.
  • Nulová hodnota zmiešaného súčinu znamená, že príslušné vektory sú komplanárne.
  • Zmiešaný súčin možno vyjadriť pomocou determinantu, pričom v jednom riadku sú súradnice jedného vektora. K tomuto tvrdeniu môžeme dospieť, keď si všimneme zápis vektorového súčinu pomocou vzťahov (1.2.16) a (1.2.17) . Ak výraz (1.2.16) skalárne vynásobíme vektorom c = cx i + cy j + cz j , dostaneme

(cx i + cy j + cz j ) × [ i ( aybz - azby ) + j ( azbx - axbz ) + k ( axby - aybx )] =

= cx ( aybz - azby ) + cy ( azbx - axbz ) + cz ( axby - aybx ),

takže je zrejmé, že tento zmiešaný súčin možno vyjadriť ako determinant

(a ´ b) = (1.2.22)

Zápisom zmiešaného súčinu v tvare determinantu možno overiť pravidlo o cyklickej zmene poradia vektorov, ako aj o zmene znamienka pri zámene poradia dvoch vektorov. Zámena poradia dvoch vektorov sa v determinante prejaví ako zámena dvoch riadkov, ktorej dôsledkom je zmena znamienka determinantu.

Príklad 1.2.5 Vypočítajte zmiešaný súčin c × (a ´ b) pričom vektory sú zadané v zložkovom tvare : a = 5 i , b = 4 i + 3 j , c = 2 i - j + k . Presvedčte sa, že rovnaký výsledok dostanete, ak v zmiešanom súčine urobíte cyklickú zámenu poradia vektorov.

Riešenie: Výpočtom vektorového súčinu sa presvedčíme, že (a ´ b) = 15 k . Výsledok vynásobíme skalárne vektorom c : (15 k ) × (2 i - j + k ) = 15 .

Pre zmiešaný súčin (c ´ a) × b dostaneme rovnaký výsledok : (2 i - j + k ) ´ (5i ) = 5k + 5 j a ďalej (5k + 5 j ) × (4 i + 3 j ) = 15 .

Dvojnásobný vektorový súčin medzi tromi vektormi a, b, c môže mať dva tvary , pokiaľ dodržíme určené poradie vektorov :

a ´ (b ´ c) a (a ´ b) ´ c (1.2.23)

Zo zápisu je zrejmé, že výsledkom dvojnásobného vektorového súčinu je vektorová veličina. Uvedené dva tvary neposkytujú rovnaký výsledok. Výsledkom súčinu vektorov nachádzajúcich sa v zátvorke je v oboch prípadoch vektor , ktorý je na ich rovinu kolmý (označme si ho ako w , obr. 1.2.5). Súčinom vektora w s ďalším vektorom je vektor u, ktorý je kolmý aj na vektor w, takže u musí ležať v rovine vektorov, ktoré sú uvedené v zátvorke. To znamená, že výsledok dvojnásobného vektorového súčinu u možno vyjadriť ako lineárnu kombináciu vektorov, nachádzajúcich sa v zátvorke. V prvom prípade výsledný vektor u1 leží v rovine vektorov b, c a v druhom prípade výsledný vektor u2 leží v rovine vektorov a, b .

Pre výsledné vektory platia nasledujúce vzorce :

u1 = a ´ (b ´ c) = b (a × c) - c (a × b ) (1.2.24) u2 = (a ´ b) ´ c = b (a × c) - a (b × c ) (1.2.25)

Správnosť týchto vzorcov možno dokázať celkom všeobecným postupom, ktorý je však náročný a pomerne rozsiahly. Preto si jeden zo vzorcov, a to (1.2.25) , odvodíme zjednodušeným postupom na príklade troch ľubovoľných nekomplanárnych vektorov a, b, c, v špeciálne zvolenej karteziánskej súradnicovej sústave. Súradnicovú os x zvolíme tak, aby bola rovnobežná s vektorom a , takže a bude mať len jednu zložku, a to rovnobežnú s jednotkovým vektorom i : a = ax i . Os y zvolíme tak, aby rovina xy bola rovnobežná s rovinou určenou vektormi a, b . Vtedy vektor b , pokiaľ nie je kolmý na a , bude mať dve zložky : b = bx i + by j . Os z karteziánskej sústavy je tým už jednoznačne určená, a tak vektor c , ak chceme uvažovať čo najvšeobecnejšie, musí mať tri zložky : c = cx i + cy j + cz k

Súhrnne :a = ax i

b = bx i + by j (1.2.26)

c = cx i + cy j + cz k

Potom dvojnásobný vektorový súčin (a ´ b) ´ c vypočítame :

= [ ax i ´ (bx i + by j )] ´ (cx i + cy j + cz k ) = [ ax by k] ´ (cx i + cy j + cz k ) =

= ax by cx j - ax by cy i + ( ax bx cx i - ax bx cx i )

Výraz v zátvorke v poslednom riadku nie je výsledkom priameho výpočtu, rovná sa nule, a to, že sme ho pridali do výpočtu, je len súčasťou nášho zjednodušeného postupu. Vhodným pospájaním členov posledného riadku dostaneme :

(a ´ b) ´ c = (ax cx) (bx i + by j ) - (bx cx + by cy) (ax i) .

Keď si uvedomíme, že platí ax cx = a × c a bx cx + by cy = b × c ,

čo si ľahko overíme vypočítaním týchto skalárnych súčinov vychádzajúc zo zadania vektorov (1.2.26), dostaneme konečný výsledok

(a ´ b) ´ c = b (a × c) - a (b × c )

Podobne možno odvodiť aj vzorec (1.2.24), pričom opäť sa overí zásada, že výsledný vektor, výsledok dvojnásobného vektorového súčinu, možno vyjadriť ako lineárnu kombináciu vektorov ležiacich v rovine vektorov uvedených v zátvorke.

Dvojnásobný vektorový súčin sa často využíva pri vyjadrovaní vzťahov v mechanike, ale aj elektromagnetizme.

Príklad 1.2.6 Vypočítajte dvojnásobný vektorový súčin ( a ´ b) ´ c vektorov : a = 5 i , b = 4 i + 3 j , c = 2 i - j + k a presvedčte sa, že výsledný vektor leží v rovine vektorov a, b . Vektory a, b ležia v rovine xy , takže výsledný vektor by mal mať len zložky v smere jednotkových vektorov i, j . Nakreslite si obrázok.

Riešenie : ( a ´ b) ´ c = [ 5 i ´ ( 4 i + 3 j )] ´ (2 i - j + k ) = [ 15 k] ´ (2 i - j + k ) =

= 30 j + 15 i

 

Kontrolné otázky k časti 1.2

  1. Poznáme veľkosť dvoch vektorov a uhol medzi nimi. Čomu sa rovná ich skalárny súčin ?
  2. Aká je dohoda o maximálnej hodnote uhla medzi dvoma vektormi ?
  3. Kedy je skalárny súčin dvoch vektorov záporný ?
  4. Čomu sa rovná skalárny súčin vzájomne kolmých vektorov ?
  5. Uveďte, čomu sa rovnajú skalárne súčiny j × j a i × k !
  6. Viete vyjadriť skalárny súčin dvoch vektorov, ak poznáte ich súradnice v karteziánskej sústave ?
  7. Ako vyjadrujeme distributívnosť skalárneho súčinu ?
  8. Ako možno pomocou skalárneho súčinu vypočítať uhol medzi dvomi vektormi ?
  9. Čo rozumieme pod priemetom vektora do iného, s ním nekolineárneho vektora ?
  10. Čo predstavuje priemet vektora do jednotkového vektora v smere súradnicovej osi ?
  11. Akú veľkosť má vektor, ktorý vznikne ako vektorový súčin dvoch vektorov ?
  12. Aký smer má vektor, ktorý vznikne ako vektorový súčin dvoch vektorov ?
  13. Čo znamená, ak trojica vektorov tvorí pravotočivú sústavu ?
  14. Ako vytvoríme z pravotočivej sústavy troch vektorov ľavotočivú sústavu ?
  15. Je vektorový súčin komutatívna operácia ?
  16. Aký je geometrický význam vektorového súčinu dvoch vektorov ?
  17. Dokážete vyjadriť všetky možné kombinácie vektorových súčinov medzi vektormi i, j, k ?
  18. Ako vyjadrujeme distributívnosť vektorového súčinu ?
  19. Viete vyjadriť vektorový súčin v tvare determinantu ?
  20. Pri násobení vektorového súčinu skalárom - možno vopred skalárom vynásobiť niektorý z vektorov súčinu, alebo až výsledný vektor ?
  21. Uveďte možné varianty zmiešaného súčinu troch vektorov !
  22. Aký je geometrický význam zmiešaného súčinu ? Zdôvodnite svoje tvrdenie !
  23. Viete zdôvodniť pravidlo o posune zátvoriek a súčasnej zámene "bodky a krížika" v zmiešanom súčine ?
  24. Kedy je zmiešaný súčin kladný, záporný, nulový ?
  25. Vyjadrite zmiešaný súčin troch vektorov v tvare determinantu !
  26. Čo sa zmení na zmiešanom súčine, ak v ňom zmením poradie dvoch vektorov ?
  27. Napíšte dva možné varianty dvojnásobného vektorového súčinu !
  28. V ktorej rovine leží výsledný vektor dvojnásobného vektorového súčinu ? Zdôvodnite svoje tvrdenie !
  29. Napíšte vzorce vyjadrujúce výsledný vektor získaný dvojnásobným vektorovým súčinom !

Príklad 1.2.2 Určte plošný obsah trojuholníka určeného vektormi a = 5 i a b = 4 i + 3 j . (Pozri príklad 1.2.1 , kde je obrázok)

Riešenie : Veľkosť vektorového súčinu a ´ b predstavuje plošný obsah rovnobežníka vytvoreného pomocou týchto vektorov, plošný obsah trojuholníka je jeho polovicou. Mohli by sme postupovať tak, že vypočítame veľkosti vektorov a, b a uhol medzi nimi (pomocou vzorca (1.2.7)) , vypočítame veľkosť vektorového súčinu ab sina a vydelíme ho dvomi. Pri šikovnejšom postupe najprv vypočítame výsledný vektor u = a ´ b :

u = (5 i) ´ (4 i + 3 j ) = (5 × 4)(i ´ i) + (5 × 3)(i ´ j) = 15 k ,

a z výsledku bezprostredne vidíme, že veľkosť vektora u je 15. Preto plošný obsah trojuholníka je 7,5 jednotiek.

Príklad 1.2.3 V priestore sú zadané tri body A(2,0,0), B(0,1,0), C(0,0,3) , ktorými je určená rovina. Vyjadrite jednotkový vektor kolmý na túto rovinu. Nakreslite si obrázok !

Riešenie : Základnou ídeou riešenia je využitie vektorového súčinu, ktorého výsledkom je vektor kolmý na rovinu násobených vektorov. Preto stačí nájsť dva vektory, ktoré ležia v príslušnej rovine. Takýmito sú vektory, ktoré spájajú zadané tri body. Získame ich ako rozdiel vektorov spájajúcich začiatok súradnicovej sústavy a zadané body. Do bodu A smeruje vektor a = 2 i , do ďalších bodov vektory b = j , c = 3 k . Vektor vychádzajúci z bodu A a končiaci v bode B je u = b - a = j - 2 i , vektor vychádzajúci z bodu A a končiaci v bode C je w = c - a = 3 k - 2 i . Potom vypočítame vektorový súčin h = u ´ w = ( j - 2 i) ´ ( 3 k - 2 i ) = 3 i + 2 k + 6 j . Výsledný vektor h je kolmý na rovinu prechádzajúcu bodmi A, B, C . Jednotkový vektor kolmý na túto rovinu získame, ak vektor h vydelíme jeho veľkosťou

h =. Pre jednotkový vektor tak dostaneme :