




Základné informácie o vektoroch
Vo fyzike a technických disciplínach sa stretávame s veličinami, na úplné určenie ktorých postačuje zadať jedinú číselnú hodnotu. Pre takéto veličiny, medzi ktoré patria napr. teplota, hmotnosť, alebo objem, používame názov skalárne veličiny (stručne
skaláry ). Často sa však stretávame s veličinami, ktoré charakterizujeme nie iba ich veľkosťou, ale aj smerom v priestore. Nazývame ich vektorové veličiny (stručne vektory ). Navyše je pre ne typický spôsob sčitovania, ktorý geometricky znázorňujeme pomocou skladania úsečiek. Medzi vektorové veličiny patrí napríklad rýchlosť , sila, alebo intenzita elektrického poľa . Na úplné určenie vektorovej veličiny v trojrozmernom priestore, vzhľadom na potrebu vyjadriť nie iba jej veľkosť, ale aj smer, treba zadať tri číselné hodnoty, ktorým hovoríme súradnice vektora ( vektorové súradnice ).
Vektory sa zapisujú tučnými písmenami, napr. a , E , r , alebo označujú šipkou nad písmenom : . Značky všetkých veličín, teda aj vektorových, sa podľa normy STN ISO 31-0 majú písať ležatým písmom - kurzívou . Veľkosť vektorových veličín sa zapisuje jednoduchým písmom (nie tučným, resp. bez šipky nad písmenom) : b, E, f , alebo sa vektor vloží mezi značky vyjadrujúce absolútnu hodnotu :
|ā|, |E|, resp.|f| . Veľkosť vektora sa nazýva aj absolútna hodnota, je vždy nezáporná .
Graficky sa vektorové veličiny znázorňujú úsečkou, so šipkou na jednom konci úsečky.
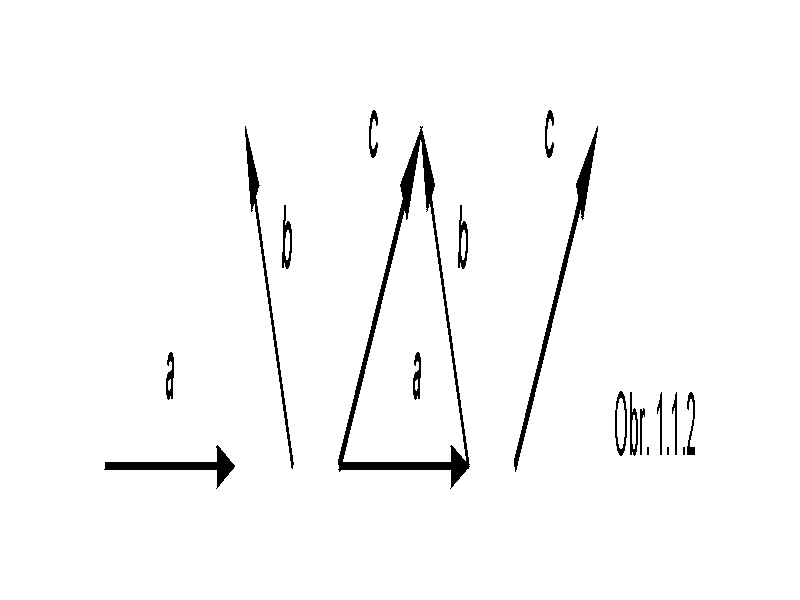 Miesto na úsečke opatrené šipkou sa považuje za "koniec vektora", na opačnej strane úsečky je "začiatok vektora".
Miesto na úsečke opatrené šipkou sa považuje za "koniec vektora", na opačnej strane úsečky je "začiatok vektora".
Vektory rovnobežné s jednou priamkou nazývame kolineárne, vektory rovnobežné s jednou rovinou komplanárne. Kolineárne vektory môžu mať rovnaký, alebo navzájom opačný smer.
Dva vektory považujeme za rovnaké, ak majú rovnaký smer a rovnakú veľkosť (sú teda kolineárne) .
|