




1.2 Súčiny medzi vektormi
Vektorová algebra popri násobení vektorov skalármi zavádza aj
súčiny medzi vektormi.
Skalárny súčin dvoch vektorov je zavedený ako
operácia, ktorej výsledkom je skalárna veličina. Hodnota tejto skalárnej veličiny je
určená súčinom veľkostí príslušných vektorov a kosínusu uhla, ktorý tieto
vektory zvierajú. Fyzikálny rozmer výslednej skalárnej veličiny sa rovná súčinu
rozmerov násobených vektorových veličín. Skalárny súčin sa označuje bodkou medzi
vektormi, v strede výšky písmen (nie na úrovni riadku) :
a × b = ab cos
a . (1.2.1)
Pritom uhol medzi dvoma vektormi sa
určuje tak, aby nebol väčší ako p radiánov (180 o). Bezpečne ho určíme tak, keď oba vektory nakreslíme so
spoločným začiatkom.
Niektoré vlastnosti skalárneho
súčinu
- Skalárny súčin je komutatívny, čo vyplýva bezprostredne z jeho definície :
a × b = b
× a (1.2.2)
- Skalárny súčin môže byť kladný i záporný, čo závisí od hodnoty uhla medzi
vektormi. Ak je uhol medzi vektormi menší ako p /2, skalárny
súčin je kladný, lebo kosínus ostrého uhla je kladný. Pri uhle väčšom ako p /2, je kosínus uhla, a teda aj skalárny súčin, záporný.
- Ak sa skalárny súčin dvoch vektorov rovná nule, pričom
ani jeden z vektorov nemá nulovú veľkosť, vektory sú na seba kolmé, lebo cos (p /2) = 0.
- Skalárny súčin vektora so sebou samým : a ×
a = aa cos 0 = a2 .
V tomto prípade sa používa aj označenie a × a = a2 .
- Pre skalárne súčiny medzi jednotkovými vektormi i, j, k karteziánskej súradnicovej sústavy platia vzťahy
i × i = 1 , j × j = 1 , k × k =
1 , i × j = 0 , i ×
k = 0, j × k = 0 (1.2.3)
- Pre skalárny súčin platí di
stributívny zákon :
a × (b + c) = a
× b + a × c(1.2.4)
alebo všeobecnejšie :
(a1 + a2 + … + ap)
× (b1 + b2 +
…+ bq) = a1 × b1
+ a1 × b2
+…+ a1× bq +
… + ap × bq
- Skalárny súčin vektorov vyjadrených pomocou súradníc, teda ako lineárna
kombinácia vektorov
i, j, k , možno vypočítať s využitím distributívneho zákona takto
:
a × b = (ax i
+ ay j + az k) × (bx i + by j + bz
k ) = ax bx + ay by + az
bz , (1.2.5)
napríklad (3 i + 2 j -
k) × (-
i + 2 j - 2 k ) = - 3 + 4 + 2 = 3 .
- Z definície skalárneho súčinu vyplýva vzťah
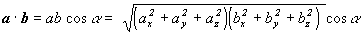 , (1.2.6) , (1.2.6)
takže porovnaním (1.2.5) a (1.2.6) môžeme získať vzorec na
výpočet (kosínusu) uhla medzi vektormi :
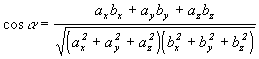
(1.2.7)
- Skalárny súčin možno využiť na výpočet súradnice vektora v karteziánskej
sústave, ak vektor vynásobíme príslušným jednotkovým vektorom. Použitím
distributívneho zákona (1.2.4) a vzťahov (1.2.3) dostaneme napríklad
j × (ax i + ay j
+ az k) = ay .
Podobne získame ostatné súradnice, takže platí :
ax = a × i
, ay = a × j , az
= a × k (1.2.8)
- Pomocou týchto vzťahov možno vytoriť zložky vektora
a v smere súradnicových osí v karteziánskej sústave, t.j.
rozložiť ho na tieto zložky. Ide vlastne o ortogonálne priemety s , t a
u vektora a do smerov súradnicových
osí, t.j. do smerov určených jednotkovými vektormi i, j, k
. Platí pre ne :
s = ax i = (a × i) i , t = ay j =
(a × j) j , u = az
k = (a × k) k
(1.2.9)
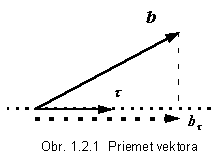
Tento postup môže poslúžiť aj pri vytváraní ortogonálneho priemetu
vektora do ľubovoľného smeru v priestore, určeného
jednotkovým vektorom. Napríklad priemet bt (na obr. 1.2.1 čiarkovaný) vektora b do
smeru jednotkového vektora t získame
tak, že vypočítame ich skalárny súčin a takto získaným skalárom vynásobíme
vektor t :
bt = (b × t )t
(1.2.10)
Skalárny súčin sa často využiva v mechanike, a teórii
elektromagnetického poľa. Napríklad skalárnym súčinom vektora sily f a
vektora elementárneho posunutia dr sa vyjadruje elementárna práca dW
= f × dr = f dr cos a , lebo smer sily a smer posunutia
telesa nemusia byť rovnaké. Vtedy sa na vykonanie práce využíva iba priemet
sily do smeru posunutia, vyjadrený ako f cosa .
Príklad 1.2.1 Na obr.1.2.2 je
znázornený trojuholník určený vektormi a = 5i , b = 4i
+ 3j . Vypočítajte uhly medzi stranami a , b
a stranami a, c .
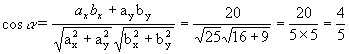
čiže a = 36,9o . Na výpočet
uhla b potrebujeme vyjadriť vektor c = b - a = - i + 3j a
opäť použiť vzorec (1.2.7). Musíme si však uvedomiť, že 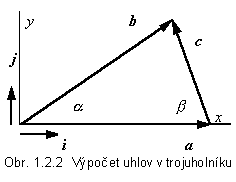 vektor a s
vektorom c zviera uhol g = 180o
- b . Tak dostaneme : vektor a s
vektorom c zviera uhol g = 180o
- b . Tak dostaneme :
cos g = - 1/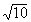 , čiže g = 108,43 o
. , čiže g = 108,43 o
.
Vektorový súčin dvoch vektorov je operácia, ktorej výsledkom je vektor. Preto treba definovať
nie iba veľkosť výsledku, ale aj smer
výsledného vektora. Vektorový súčin sa označuje krížikom medzi vektormi :
c = a ´ b(1.2.11)
Veľkosť c výsledného vektora c je definovaná ako súčin veľkostí násobených vektorov a
sínusu uhla nimi zovretého :
c = ab sina (1.2.12)
Pre smer vektora c platí
definícia, že je kolmý na rovinu násobených vektorov. Jednoznačnosť definície
však vyžaduje určiť, na ktorú stranu roviny smeruje. Vektor c má taký smer, že z jeho konca sa stotožnenie prvého
vektora zo súčinu (v tomto prípade vektora a) s druhým vektorom po kratšom oblúku javí ako pohyb proti
chodu hodinových ručičiek. O trojici vektorov a, b, c v danom poradí potom hovoríme, že tvoria pravotočivú
sústavu vektorov. Zmena ich poradia jednou permutáciou znamená zmenu
z pravotočivej na ľavotočivú sústavu (trojicu).
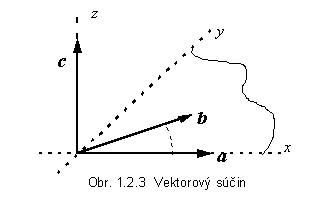
Na obr. 1.2.3 je trojica vektorov a, b, c znázornená v axonometrickom pohľade. Pre názornosť sú
nakreslené aj súradnicové osi karteziánskej sústavy. Ak otáčanie vektora a
k vektoru b po kratšom oblúku
napodobíme otáčaním pravotočivej skrutky, umiestnenej v začiatku súradnicovej
sústavy kolmo na rovinu vektorov a b ,
skrutka sa bude posúvať v smere vektora c . Aj tento model pomáha pri určovaní smeru vektora, ktorý je
výsledkom vektorového súčinu .
Niektoré vlastnosti vektorového
súčinu
- Vektorový súčin nie je komutatívna operácia, lebo zámena poradia vektorov
poskytuje síce vektor rovnako veľký, ale opačného smeru. Táto skutočnosť sa
zapisuje v tvare :
a ´ b = - b ´ a(1.2.13)
- Veľkosť vektorového súčinu dvoch vektorov možno interpretovať ako plošný obsah
rovnobežníka vytvoreného týmito vektormi. Navyše výsledný vektor jednoznačne
určuje orientáciu roviny v priestore, preto ho možno chápať ako vektor
priradený ploche.
- Z definície veľkosti vektorového súčinu vyplýva,
že vektorový súčin dvoch kolineárnych vektorov sa rovná nule (je nulový vektor).
- Pre jednotkové vektory i , j , k ,
ktoré sú navzájom na seba kolmé, platia vzťahy :
i ´ i = 0 j ´ j = 0 k ´ k = 0
(1.2.14)
i ´ j = k j ´ k = i k ´ i = j j ´
i = - k k ´ j = -
i i ´ k = - j
- Pre vektorový súčin platí distributívny zákon :
a ´ (b + c) = a
´ b + a ´ c (b + c)
´ a = b ´ a + c ´ a (1.2.15)
Dva prípady distributívneho zákona sú uvedené preto, lebo vo
vektorovom súčine nemožno zamieňať poradie vektorov bez zmeny znamienka.
- Na základe distributívneho zákona vektorový súčin vektorov vyjadrených v
zložkovom tvare môžeme vyjadriť nasledovne :
a ´ b = (ax i
+ ay j + az k) ´ (bx i + by j + bz
k ) =
= axbx(i ´
i) + axby(i ´ j)
+ axbz(i ´ k) +
+ aybx(j ´
i) + ayby(j ´ j)
+ aybz( j ´ k) +
+ azbx(k ´
i) + azby(k ´ j)
+ az bz(k ´ k)
=
= 0 + axby k - axbz
j +
- aybx k
+ 0 + aybz i +
+ azbx j - azby
i + 0 =
= i (aybz - azby ) + j (azbx
- axbz ) + k (axby
- aybx ) (1.2.16)
Čitateľovi, ktorý pozná determinanty je zrejmé, že posledný
výraz možno formálne vyjadriť a ko determinant :
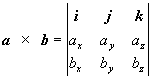 (1.2.17) (1.2.17)
Príklad 1.2.2 Určte plošný obsah
trojuholníka určeného vektormi a = 5 i a b = 4
i + 3 j . (Pozri príklad 1.2.1 , kde je obrázok)
Riešenie : Veľkosť vektorového súčinu a ´ b predstavuje plošný obsah rovnobežníka vytvoreného
pomocou týchto vektorov, plošný obsah trojuholníka je jeho polovicou. Mohli by sme
postupovať tak, že vypočítame veľkosti vektorov a, b a uhol medzi nimi
(pomocou vzorca (1.2.7)) , vypočítame veľkosť vektorového súčinu ab sina a vydelíme ho dvomi. Pri šikovnejšom postupe najprv vypočítame
výsledný vektor u = a ´ b :
u = (5 i) ´ (4
i + 3 j ) = (5 × 4)(i ´ i) + (5 × 3)(i ´ j) = 15 k ,
a z výsledku bezprostredne vidíme, že veľkosť vektora u
je 15. Preto plošný obsah trojuholníka je 7,5 jednotiek.
Príklad 1.2.3 V priestore sú zadané tri body A(2,0,0),
B(0,1,0), C(0,0,3) , ktorými je určená rovina. Vyjadrite jednotkový vektor kolmý na
túto rovinu. Nakreslite si obrázok !
Riešenie : Základnou ídeou riešenia je využitie vektorového
súčinu, ktorého výsledkom je vektor kolmý na rovinu násobených vektorov. Preto
stačí nájsť dva vektory, ktoré ležia v príslušnej rovine. Takýmito sú vektory,
ktoré spájajú zadané tri body. Získame ich ako rozdiel vektorov spájajúcich
začiatok súradnicovej sústavy a zadané body. Do bodu A smeruje vektor a = 2
i , do ďalších bodov vektory b = j , c = 3 k .
Vektor vychádzajúci z bodu A a končiaci v bode B je u = b - a = j -
2 i , vektor vychádzajúci z bodu A a končiaci v bode C je w = c -
a = 3 k - 2 i . Potom vypočítame vektorový súčin h
= u ´ w = ( j - 2 i)
´ ( 3 k - 2 i ) = 3 i + 2
k + 6 j . Výsledný vektor h je kolmý na
rovinu prechádzajúcu bodmi A, B, C . Jednotkový vektor kolmý na túto rovinu získame,
ak vektor h vydelíme jeho veľkosťou
h =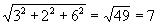 . Pre jednotkový
vektor tak dostaneme : . Pre jednotkový
vektor tak dostaneme :
ho = h / 7 = (3/7) i
+ (2/7) j + (6/7) k .
S vektorovým súčinom sa stretneme napríkla d pri vyjadrení
momentu sily M = r ´ f, kde r
je polohový vektor pôsobiska sily f , alebo
pri vzťahu pre silu f pôsobiacu na elektrický náboj q
pohybujúci sa v magnetickom poli s magnetickou indukciou B : f = qv ´ B .
Príklad 1.2.4 Vypočítajte skalárny násobok vektorového
súčinu vektorov a = 5 i , b = 4 i + 3
j z príkladu (1.2.2) skalárom p = 2 .
Riešenie : pc = p(a ´ b ) = p[ (5i)
´ (4 i + 3 j)]
= p (15 k) = 30 k .
Poznámka : Rovnaký výsledok dostaneme, ak skalárom p
vynásobíme niektorý z vektorov a, b ešte pred uskutočnením
vektorového súčinu :
a) pc = p(a ´
b ) = (pa ´ b) = (10 i)
´ (4 i + 3 j) = 30 k
b) pc = p(a ´
b ) = (a ´ pb) = (5 i)
´ (8 i + 6 j) = 30 k
Z výsledku vyplýva významné pravidlo, že nezáleží na tom,
ktorému z vektorov vektorového súčinu priradíme skalár, ktorým vektorový súčin
násobíme.
Zmiešaný súčin troch vektorov je
operácia, v ktorej sa uskutoční najprv vektorový a po
ňom skalárny súčin. Medzi tromi vektormi a, b, c je možných viacero variantov zmiešaného súčinu, napríklad :
a × (b ´ c), (a ´ b) × c , (b ´ c)
× a (1.2.18)
Výsledkom je vždy skalárna veličina, ktorá môže byť kladná,
nulová i záporná.
Niektoré vlastnosti zmiešaného
súčinu .
- Výraz (a × b) ´ c , nie je zmiešaný súčin, lebo výraz v zátvorke je
skalárna veličina, ktorou nemožno vektor c násobiť vektorovo.
- Zmiešaný súčin má význam objemu rovnobežnostena skonštruovaného na základe
vektorov zmiešaného súčinu. Na obrázku 1.2.5 je nakreslený rovnobežnosten
zostrojený pomocou vektorova, b, c , ako aj priamka z
kolmá na rovinu vektorov a, b . Zmiešaný
súčin
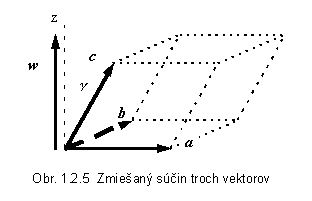
S = (a ´ b) × c vypočítame podľa
pravidiel vektorového a skalárneho súčinu . Výsledkom vektorového súčinu a
´ b je vektor (označme
ho w) kolmý na ich rovinu, teda vektor,
ktorý má veľkosť ab sina a je rovnobežný s priamkou z . Vektor w
zviera s vektorom c uhol g , ktorého kosínus vstupuje do výrazu pre skalárny súčin medzi
vektormi w a c . Pre
výsledok zmiešaného súčinu tak dostaneme S = (ab sina ) c cosg . Výraz c cosg súčasne predstavuje výšku
rovnobežostena, pričom veľkosť vektorového súčinu ab sina je plošný obsah jeho základne.
Preto zmiešaný súčin má význam objemu rovnobežnostena.
- Objem toho istého rovnobežnostena dostaneme aj pomocou zmiešaných súčinov (b
´ c) × a
a (c ´ a) × b , teda súčinmi, v ktorých sme urobili cyklickú zámenu
poradia vektorov, pri zachovaní polohy zátvoriek, ako aj značiek vektorového a
skalárneho súčinu. Preto platia rovnosti
(a ´ b) ×
c = (b ´ c) × a = (c ´ a)
× b (1.2.19)
- Ak si uvedomíme komutatívnosť skalárneho súčinu, môžeme napísať rovnosť
(a ´ b) ×
c = c × (a ´ b ) (1.2.20) Porovnaním
posledných členov rovností (1.2.19) a (1.2.20) dostaneme výsledok
(c ´ a) ×
b = c × (a ´ b
) (1.2.21)
ktorý interpretujeme ako možnosť premiestnenia zátvoriek, pri
súčasnej výmene značiek vektorového a skalárneho súčinu.
- Zmiešaný súčin je kladný, ak vektory v zmiešanom súčine, v takom
poradí ako sú napísané, tvoria pravotočivú sústavu. Zámenou poradia ľubovoľných
dvoch vektorov v zmiešanom súčine, zmení sa jeho znamienko. Ak je zmiešaný
súčin záporný, objemu rovnobežnoste
na sa vtedy rovná jeho absolútna hodnota.
Nulová hodnota zmiešaného súčinu znamená, že príslušné vektory sú
komplanárne.
Zmiešaný súčin možno vyjadriť pomocou determinantu, pričom v jednom riadku sú
súradnice jedného vektora. K tomuto tvrdeniu môžeme dospieť, keď si všimneme
zápis vektorového súčinu pomocou vzťahov (1.2.16) a (1.2.17) . Ak výraz (1.2.16)
skalárne vynásobíme vektorom c = cx i + cy
j + cz j , dostaneme
(cx i + cy j + cz
j ) × [ i ( aybz
- azby ) + j (
azbx - axbz
) + k ( axby - aybx
)] =
= cx ( aybz - azby ) + cy (
azbx - axbz
) + cz ( axby - aybx
),
takže je zrejmé, že tento zmiešaný súčin možno vyjadriť ako
determinant
(a ´ b) =  (1.2.22) (1.2.22)
Zápisom zmiešaného súčinu v tvare determinantu možno overiť
pravidlo o cyklickej zmene poradia vektorov, ako aj o zmene znamienka pri zámene poradia
dvoch vektorov. Zámena poradia dvoch vektorov sa v determinante prejaví ako zámena
dvoch riadkov, ktorej d ôsledkom je zmena znamienka determinantu.
Príklad 1.2.5 Vypočítajte zmiešaný
súčin c × (a ´
b) pričom vektory sú zadané v zložkovom tvare : a = 5 i
, b = 4 i + 3 j , c = 2 i
- j + k . Presvedčte sa, že rovnaký výsledok dostanete, ak
v zmiešanom súčine urobíte cyklickú zámenu poradia vektorov.
Riešenie: Výpočtom vektorového súčinu sa presvedčíme, že (a
´ b) = 15 k . Výsledok vynásobíme
skalárne vektorom c : (15 k ) ×
(2 i - j + k ) = 15 .
Pre zmiešaný súčin (c ´ a)
× b dostaneme rovnaký výsledok : (2 i
- j + k ) ´ (5i ) =
5k + 5 j a ďalej (5k + 5 j ) × (4 i + 3 j ) = 15 .
Dvojnásobný vektorový súčin medzi tromi vektormi a,
b, c môže mať dva tvary , pokiaľ dodržíme
určené poradie vektorov :
a ´ (b ´
c) a (a ´ b) ´
c (1.2.23)
Zo zápisu je zrejmé, že výsledkom dvojnásobného vektorového
súčinu je vektorová veličina. Uvedené dva tvary neposkytujú rovnaký výsledok.
Výsledkom súčinu vektorov nachádzajúcich sa v zátvorke je v oboch prípadoch vektor
, ktorý je na ich rovinu kolmý (označme si ho ako w , obr. 1.2.5). Súčinom vektora w s ďalším vektorom je vektor u, ktorý je
kolmý aj na vektor w, takže u musí ležať v rovine vektorov, ktoré sú uvedené
v zátvorke. To znamená, že výsledok dvojnásobného vektorového súčinu u možno vyjadriť ako lineárnu kombináciu vektorov,
nachádzajúcich sa v zátvorke. V prvom prípade výsledný vektor u1 leží v rovine vektorov b, c a
v druhom prípade výsledný vektor u2 leží v rovine vektorov a, b .
Pre výsledné vektory platia nasledujúce vzorce :
u1 = a ´ (b
´ c) = b (a × c) - c (a ×
b ) (1.2.24) u2 = (a ´
b) ´ c = b (a
× c) - a (b × c ) (1.2.25)
Správnosť týchto vzorcov možno dokázať celkom všeobecným
postupom, ktorý je však náročný a pomerne rozsiahly. Preto si jeden zo vzorcov, a to
(1.2.25) , odvodíme zjednodušeným postupom na príklade troch ľubovoľných
nekomplanárnych vektorov a, b, c, v špeciálne zvolenej
karteziánskej súradnicovej sústave. Súradnicovú os x zvolíme tak, aby bola rovnobežná s vektorom a , takže a bude
mať len jednu zložku, a to rovnobežnú s jednotkovým vektorom i :
a = ax i . Os y zvolíme tak, aby rovina xy bola rovnobežná s rovinou určenou vektormi a, b
. Vtedy vektor b , pokiaľ nie je kolmý na a
, bude mať dve zložky : b
= bx i + by j . Os z karteziánskej sústavy je tým už jednoznačne určená, a tak
vektor c , ak chceme uvažovať čo
najvšeobecnejšie, musí mať tri zložky : c = cx i
+ cy j + cz k
Súhrnne :a = ax i
b = bx i + by j
(1.2.26)
c = cx i + cy j
+ cz k
Potom dvojnásobný vektorový súčin ( a ´ b) ´ c vypočítame :
= [ ax i ´ (bx i + by j
)] ´ (cx i
+ cy j + cz k ) = [
ax by k] ´ (cx i + cy j + cz
k ) =
= ax by cx j - ax by cy i +
( ax bx cx i - ax
bx cx i )
Výraz v zátvorke v poslednom riadku nie je výsledkom priameho
výpočtu, rovná sa nule, a to, že sme ho pridali do výpočtu, je len súčasťou
nášho zjednodušeného postupu. Vhodným pospájaním členov posledného riadku
dostaneme :
(a ´ b) ´ c = (ax cx) (bx
i + by j ) - (bx
cx + by cy) (ax i)
.
Keď si uvedomíme, že platí ax cx
= a × c a bx cx
+ by cy = b × c ,
čo si ľahko overíme vypočítaním týchto skalárnych súčinov
vychádzajúc zo zadania vektorov (1.2.26), dostaneme konečný výsledok
(a ´ b) ´ c = b (a × c) - a (b
× c )
Podobne možno odvodiť aj vzorec (1.2.24), pričom opäť sa overí
zásada, že výsledný vektor, výsledok dvojnásobného vektorového súčinu, možno
vyjadriť ako lineárnu kombináciu vektorov ležiacich v rovine vektorov
uvedených v zátvorke.
Dvojnásobný vektorový súčin sa často využíva pri vyjadrovaní
vzťahov v mechanike, ale aj elektromagnetizme.
Príklad 1.2.6 Vypočítajte dvojnásobný vektorový súčin (
a ´ b) ´ c
vektorov : a = 5 i , b = 4 i + 3 j ,
c = 2 i - j + k a presvedčte sa,
že výsledný vektor leží v rovine vektorov a, b . Vektory a, b
ležia v rovine xy , takže výsledný vektor by mal mať len zložky v smere
jednotkových vektorov i, j . Nakreslite si obrázok.
Riešenie : ( a ´ b) ´ c = [ 5 i ´ ( 4 i + 3 j )]
´ (2 i - j + k ) = [ 15 k] ´
(2 i - j + k ) =
= 30 j + 15 i
Kontrolné otázky k časti 1.2
Poznáme veľkosť dvoch vektorov a uhol medzi nimi. Čomu sa rovná ich skalárny
súčin ?
Aká je dohoda o maximálnej hodnote uhla medzi dvoma vektormi ?
Kedy je skalárny súčin dvoch vektorov záporný ?
Čomu sa rovná skalárny súčin vzájomne kolmých vektorov ?
Uveďte, čomu sa rovnajú skalárne súčiny j ×
j a i × k !
Viete vyjadriť skalárny súčin dvoch vektorov, ak poznáte ich
súradnice v karteziánskej sústave ?
Ako vyjadrujeme distributívnosť skalárneho súčinu ?
Ako možno pomocou skalárneho súčinu vypočítať uhol medzi dvomi vektormi
?
Čo rozumieme pod priemetom vektora do iného, s ním nekolineárneho vektora
?
Čo predstavuje priemet vektora do jednotkového vektora v smere
súradnicovej osi ?
Akú veľkosť má vektor, ktorý vznikne ako vektorový súčin dvoch
vektorov ?
Aký smer má vektor, ktorý vznikne ako vektorový súčin dvoch vektorov ?
Čo znamená, ak trojica vektorov tvorí pravotočivú sústavu ?
Ako vytvoríme z pravotočivej sústavy troch vektorov ľavotočivú sústavu
?
Je vektorový súčin komutatívna operácia ?
Aký je geometrický význam vektorového súčinu dvoch vektorov ?
Dokážete vyjadriť všetky možné kombinácie vektorových súčinov medzi
vektormi i, j, k ?
Ako vyjadrujeme distributívnosť vektorového súčinu ?
Viete vyjadriť vektorový súčin v tvare determinantu ?
Pri násobení vektorového súčinu skalárom - možno vopred skalárom
vynásobiť niektorý z vektorov súčinu, alebo až výsledný vektor ?
Uveďte možné varianty zmiešaného súčinu troch vektorov !
Aký je geometrický význam zmiešaného súčinu ? Zdôvodnite svoje
tvrdenie !
Viete zdôvodniť pravidlo o posune zátvoriek a súčasnej zámene
"bodky a krížika" v zmiešanom súčine ?
Kedy je zmiešaný súčin kladný, záporný, nulový ?
Vyjadrite zmiešaný súčin troch vektorov v tvare determinantu !
Čo sa zmení na zmiešanom súčine, ak v ňom zmením poradie dvoch
vektorov ?
Napíšte dva možné varianty dvojnásobného vektorového súčinu !
V ktorej rovine leží výsledný vektor
dvojnásobného vektorového súčinu ? Zdôvodnite svoje tvrdenie !
Napíšte vzorce vyjadrujúce výsledný vektor získaný dvojnásobným
vektorovým súčinom !
|