




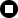
1.4 Integrácia vektorových funkcií
Najjednoduchším prípadom integrácie vektorovej funkcie je integrál typu
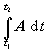 (1.4.1) (1.4.1)
v ktorom t je skalárna premenná, pričom vektorová funkcia A závisí od tejto premennej. Keď vektorovú funkciu A (t) rozpíšeme v zložkovom tvare, A = Axi + Ayj + Azk , dostaneme tri integrály skalárnych funkcií:
 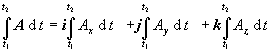  (1.4.2) (1.4.2)
Výsledkom je vektorová funkcia, závisiaca od premennej t . Príkladom je impulz sily, definovaný ako integrál sily podľa času : 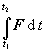 . .
Pri integrácii vektorových funkcií sa ďalej stretávame s integráciou pozdĺž krivky (krivkové integrály), a integráciou po ploche (plošné integrály).
Pri krivkových integráloch sa najčastešie stretávame s typom
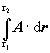 (1.4.3) (1.4.3) 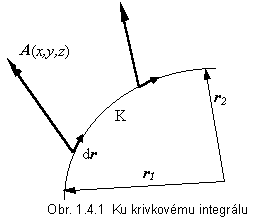
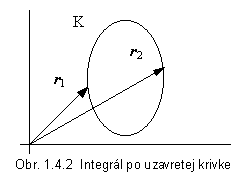
Ide o integrál vektorovej funkcie A(x,y,z) , od začiatočného bodu r1 v zvolenej súradnicovej sústave po koncový bod určený polohovým vektorom r2 . Je to v podstate súčet limitne veľkého počtu elementárnych skalárnych súčinov A ×
dr = A ds cosa
, kde A je veľkosť vektorovej funkcie (vektora) A , ds veľkosť príslušného dr a a
uhol medzi nimi v danom bode krivky, pozdĺž ktorej integrujeme (obr.1.4.1). Elementárny vektor dr má v danom bode krivky K smer jej dotyčnice. Pritom veľkosť, ani smer vektora A(x,y,z) nemusia byť konštantné, od bodu k bodu na krivke sa môžu meniť.
Takýmto integrálom sa vyjadruje napríklad práca W, pričom vektorovou funkciou je sila F :
W = 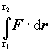 (1.4.4) (1.4.4)
Ak vektor F a diferenciál polohového vektora dr vyjadríme v zložkovom tvare, t.j.
F = Fx i + Fy j + Fz k , dr = i dx + j dy + k dz
potom po vykonaní skalárneho súčinu dostaneme
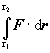 = = 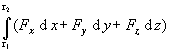 , (1.4.5) , (1.4.5)
takže ide o všeobecný krivkový integrál. Takýto tvar možno využiť pri praktickej realizácii výpočtu integrálu typu (1.4.3), keď chceme vypočítať jeho číselnú hodnotu, za predpokladu, že poznáme Fx , Fy , Fz ako funkcie premenných x, y, z . Ako integračné hranice vystupujú príslušné súradnice polohových vektorov r1 a r2
.V takejto forme možno výpočet integrálu aj naprogramovať a numericky
vypočítať.
Pri splnení určitých podmienok možno integrál typu (1.4.3) vyjadriť ako rozdiel hodnôt skalárnej funkcie v koncovom a začiatočnom bode integrácie :
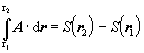 (1.4.6) (1.4.6)
To platí vtedy, ak medzi skalárnou funkciou S (x,y,z) a vektorovou funkciou A (x,y,z) platí
A = grad S , t.j.
Ax i + Ay j + Az k = (¶
S /¶
x) i + (¶
S /¶
y) j + (¶
S /¶
z) k (1.4.7)
O uvedenom tvrdení sa možno presvedčiť aj pomocou vzťahov (1.3.11) až (1.3.13) :
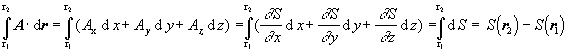
(1.4.8)
Vo vzťahoch (1.4.7) a (1.4.8) skalárna funkcia má význam potenciálu fyzikálneho poľa, vektorová funkcia význam jeho intenzity.
Príklad 1.4.1 Vypočítajme krivkový integrál funkcie F = 0 i + 0 j - mg k , ktorá reprezentuje homogénne tiažové pole v blízkom okolí povrchu Zeme, kde silu F považujeme za konštantnú - v každom bode priestoru má rovnakú veľkosť aj smer. Integrovať budeme od bodu A(x1, y1, z1) po bod B(x2, y2, z2) po krivke, ktorá spája tieto dva body.
Riešenie : Podľa rovnice (1.4.5) platí :
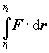 = = 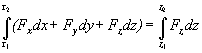 = = 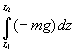 = (-mgz2) - (-mgz1) . = (-mgz2) - (-mgz1) .
Z výsledku vidno, že krivkový integrál sily F = 0 i + 0 j - mg k sa rovná rozdielu dvoch hodnôt skalárnej funkcie S (x,y,z) = -mgz , ktorá nezávisí od premenných x, y . Z výpočtu vidno, že sme nemuseli uviesť po akej krivke integrujeme, rozhodujúce sú iba začiatočný a koncový bod integrovania. Funkcia P = - S predstavuje
potenciál homogénneho gravitačného poľa.
Príklad 1.4.2 Vypočítajme krivkový integrál funkcie F = -Kr , obmezenej na jednu rovinu, t.j. nech napr. r = xi + yj . Ide vlastne o vyjadrenie dostredivej sily na otáčajúcom sa disku, lebo má smer opačný ako vektor r (ktorý má začiatok v strede otáčania) a čím ďalej od stredu otáčania, tým je sila väčšia. Integrovať budeme od bodu s polohovým vektorom r1 po bod r2 .
Riešenie : Funkciu F vyjadríme v zložkách F (x,y)= - K (xi + yj) , potom
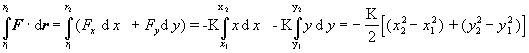 , ,
čo možno ešte upraviť na tvar zodpovedajúci rozdielu hodnôt skalárnej funkcie :
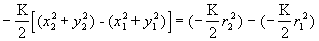 , ,
kde (r1)2 = (x1)2 +(y1)2 , (r2)2 = (x2)2 +(y2)2 .
Poznámka 1. : Na príkladoch 1.4.1 a 1.4.2 sme videli, , že výsledok nezávisí od tvaru integračnej krivky, ale len od začiatočného a koncového bodu. Ak by však vo vyjadrení funkcie F bol ešte ďalší člen, ktorý by reprezentoval napríklad trenie, potom výsledok integrácie by závisel od dĺžky konkrétne zvolenej integračnej krivky. Potom by takýto integrál nebolo možné vyjadriť ako rozdiel hodnôt skalárnej funkcie v koncovom a začiatočnom bode.
Poznámka 2. : Ak by sme v integráli (1.4.6) integrovali opačným smerom, t.j. od r2 po r1 , dostali by sme výsledok S (r1) - S (r2) , teda výsledok s opačným znamienkom. Pri integrácii po uzavretej krivke (keď začiatočný a koncový bod sú totožné) výsledok sa rovná nule, lebo na uzavretej krivke sa vyskytujú elementárne skalárne súčiny A ×
dr kladné i záporné v takom zastúpení, že výsledok ich súčtu je nulový. Takúto vlastnosť majú vektorové funkcie v oboch uvedených príkladoch. Prvá z nich predstavovala homogénne pole, druhá radiálne. Stretávame sa však aj s poľami, v ktorých integrál po uzavretej krivke nie je nulový, napr. v
magnetickom poli, ktoré má axiálny charakter. (Pozri príklad 1.3.5).
Ako bolo uvedené v príklade 1.3.5 , rotácia vektorovej funkcie predstavjúcej pole axiálneho typu nie je nulová. Vtedy možno krivkový integrál funkcie A pozdĺž uzavretej krivky nahradiť plošným integrálom rotácie funkcie A, čo vyjadruje Stokesova veta :
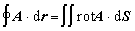 (1.4.9) (1.4.9)
Plošný integrál sa počíta cez plochu, ktorá je ohraničená integračnou krivkou K . Tvar plochy pritom nie je presne definovaný, môže to byť časť roviny, ale aj iná plocha, napríklad časť guľovej plochy, elipsoidu, či inej komplikovanejšej plochy a to aj vtedy, ak celá krivka leží v rovine. Dôkaz týchto tvrdení, vrátane dôkazu správnosti Stokesovej vety však prekračuje možnosti tohto textu. Sú predmetom matematickej analýzy.
V predošlom prípade išlo o zámenu krivkového integrálu plošným integrálom. Pod plošným integrálom vektorovej funkcie sa najčastejšie rozumie integrál, ktorý zapisujeme v tvare
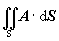 (1.4.10) (1.4.10)
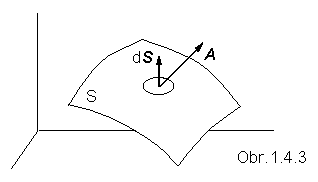
Za znakom dvojnásobného integrálu je skalárny súčin vektorovej funkcie A s diferenciálom dS ktorý ako vektor je kolmý na príslušnú elementárnu plôšku a jeho veľkosť predstavuje jej plošný obsah. Takémuto integrálu sa hovorí tok vektora A cez plochu S
. 
Aj v tomto prípade, v zmysle Riemannovej definície integrálu, ide vlastne o súčet limitne veľkého počtu elementárnych skalárnych súčinov A ×
dS = A dS cosa
, kde A je veľkosť vektorovej funkcie (vektora) A , dS veľkosť príslušného dS a a
uhol medzi nimi v danom bode plochy, pričom sa tieto súčiny sčítajú po celej ploche, po ktorej integrujeme. Veľkosť, ani smer vektora A(x,y,z) nemusia byť konštantné, od bodu k bodu na ploche sa môžu meniť. Keď dS vyjadríme v zložkách : dS = i dydz + j dzdx + k dxdy , skalárny súčin A ×
dS
možno vyjadriť aj v tvare podobnom (1.4.5) :
A ×
dS = Ax dydz + Ay dzdx + Az dxdy ,
takže integrál (1.4.10) možno vo vhodnom prípade rozpísať ako súčet troch integrálov. Výsledkom tohto integrálu je skalárna funkcia.
Ako príklad možno uviesť vzťah medzi elektrickým prúdom I a vektorom prúdovej hustoty j :
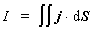
V teórii poľa sa často stretávame s plošným integrálom cez uzavretú plochu
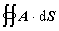 (1.4.11) (1.4.11)
ktorý pomocou Gaussovej - Ostrogradského vety možno premeniť na objemový integrál divergencie vektorovej funkcie A :
 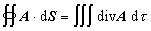 (1.4.12) (1.4.12)
kde dt
predstavuje objemový element, ktorý v karteziánskej súradnicovej sústave má tvar dt
= dx dy dz . Pod uzavretou plochou pritom rozumieme napríklad povrch gule, elipsoidu, alebo iného útvaru, tvoriaceho rozhranie medzi vnútorným a vonkajším priestorom. Podľa dohody sa elementárne plošné vektory dS orientujú vždy z uzavretej plochy von. Ani túto, veľmi významnú vetu, neodvodíme.
Kontrolné otázky k časti 1.4
Uveďte čo rozumiete pod integrálom vektorovej funkcie
a aké možné prípady poznáte !
Napíšte príklad krivkového integrálu
vektorovej funkcie !
Kedy krivkový integrál vektorovej funkcie nezávisí od tvaru krivky,
ale len od začiatočného a koncového bodu ?
Kedy sa integrál vektorovej funkcie po
uzavretej krivke nerovná nule ?
Čo hovorí Stokesova veta ?
Čo rozumiete pod plošným integrálom
vektorovej funkcie ?
Napíšte Gaussovu - Ostrogradského vetu !
|