·       Tangenciálne a normálové zrýchlenie

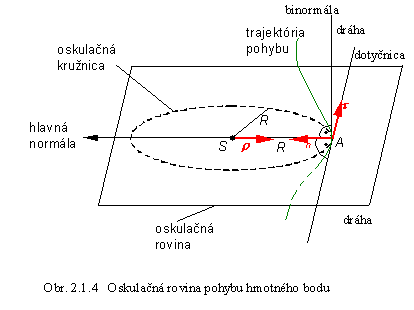
             Najvšeobecnejším pohybom hmotného bodu A je pohyb v priestore. Avšak ak zoberieme do úvahy len veľmi blízke okolie bodu A, dva vybrané body spolu s bodom A určujú rovinu, v ktorej pohyb hmotného bodu  po určitej trajektórii prebieha. Túto rovinu nazývame oskulačnou rovinou (obr. 2.1.4). Pri všeobecnom krivočiarom pohybe leží vektor zrýchlenia v danom bode A trajektórie v oskulačnej rovine, ktorá je určená dotyčnicou a hlavnou normálou trajektórie v  tomto bode. Každú krivku, po ktorej pohyb prebieha môžeme pre veľmi malé časové úseky (v limitnom prípade Dt ® 0 )  nahradiť pohybom po kružnici, ktorú nazývame oskulačnou  kružnicou.

 

             

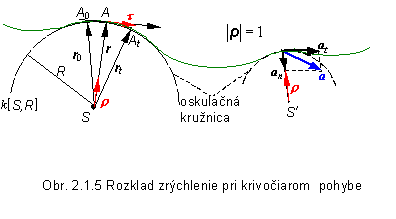
            Býva užitočné rozložiť vektor zrýchlenia v rovine oskulačnej kružnice, určenej stredom S  a polomerom krivosti R , do dvoch smerov (obr. 2.1.5):

·     do smeru dotyčnice k oskulačnej kružnici v bode A, určenej jednotkovým vektorom t ;

·     do  smeru kolmého na dotyčnicu k oskulačnej kružnici v bode A ( t.j. v smere hlavnej normály určenej jednotkovým vektorom n ), avšak určeného jednotkovým vektorom r, ktorý má začiatok v strede oskulačnej kružnice S. (Jednotkové vektory n a r majú opačný smer.)

 

 

Rozklad vektora zrýchlenia a v oskulačnej rovine  môžeme matematicky zapísať

 

a = a_t + a_n                                                                                                                        (2.1.21)

 

kde a_t nazývame tangenciálne zrýchlenie, a_n normálové (dostredivé) zrýchlenie.  Tangenciálne zrýchlenie je určené rovnicou

 

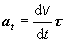                                                                                                                        (2.1.22)

 

a normálové zrýchlenie rovnicou

 

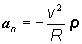                                                                                                                    (2.1.23)

 

Odvodenie týchto rovníc vyplýva z nasledovnej úvahy: Ak do vzťahu (2.1.17), ktorý definuje zrýchlenie,  dosadíme za rýchlosť bodu v rovnicu (2.1.11) ,  dostávame

 

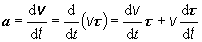                                                                                       (2.1.24)

 

pričom sme využili pravidlo pre derivovanie súčinu dvoch funkcií.

            Prvý člen v rovnici je vektor, ktorého  veľkosť sa rovná zmene veľkosti  rýchlosti za jednotku času. Smer tohto vektora má  smer dotyčnice ku dráhe a preto  prvý člen v rovnici (2.1.24) určuje  tangenciálne zrýchlenie. Veľkosť tangenciálneho zrýchlenia, a _t = dv/dt môže byť kladná aj záporná.

            Druhý člen v rovnici (2.1.24), ktorý udáva normálovú zložku zrýchlenia, možno objasniť nasledovnou úvahou:

 

 

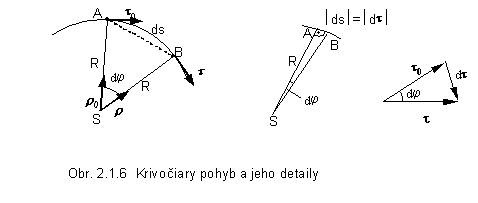
Nech sa hmotný bod v čase t₀ nachádza v bode A  (obr. 2.1.6)  a má rýchlosť určenú smerom jednotkového  vektora t₀. Za malý časový interval 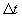 sa hmotný bod dostane do polohy určenej bodom B, v ktorom má smer rýchlosti určený jednotkovým vektorom t. Za časový interval t opísal sprievodič malý uhol da. Keďže t₀  je kolmý na jednotkový vektor r₀  a t je kolmý na jednotkový vektor r , uhol da medzi vektormi r₀  a r je ten istý i medzi vektormi  t₀  a t. Pre veľmi malú zmenu dj platí

 

dj= |dt|      resp.     

 

 

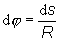
Poznámka: Pri odvodzovaní sme využili  skutočnosti:

·     sínus veľmi malého uhla možno  nahradiť týmto uhlom t.j. platí  rovnica  sin (dj ) = dj

·     trajektóriu hmotného bodu ds po krivke môžeme pri veľmi malej zmene uhla dj  nahradiť úsečkou o veľkosti ds,

·     goniometrická funkcia sínus uhla v pravouhlom trojuholníku ABS je pomer protiľahlej odvesny ku prepone.

Porovnaním posledne uvedených rovníc dostávame pre veľkosť vektora dt  vzťah

 

 

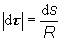
 Smer vektora dt  vyplýva z výsledku diferencovania skalárneho súčinu, daného rovnicou

 

t .t = 1 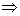                dt .t  + t . dt  = 0

 

Nakoľko skalárny súčin je komutatívny, platí

 

2t  . dt  = 0

 

Keďže ani jeden z vektorov v súčine  nie je nulový vektor a skalárny súčin sa rovná nule, znamená to, že  vektory t  a  dt sú navzájom kolmé.  Vieme, že  vektor t  je jednotkový vektor v smere dotyčnice ku trajektórii (krivke pohybu), takže vektor dt  má smer normály na túto dotyčnicu a smeruje do stredu kružnice ( Pozor! Vektor dt  má smer opačný  ako vektor r.) Po tejto úvahe  normálovú zložku zrýchlenia možno napísať v tvare

 

 

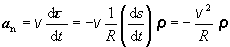
ktorý je zhodný s  tvarom  pre normálové zrýchlenie daný rovnicou (2.1.23). Pretože normálové zrýchlenie smeruje do okamžitého stredu krivosti čiary pohybu,  nazýva sa aj zrýchlením dostredivým.

Pre absolútnu hodnotu celkového zrýchlenia  platí rovnica

 

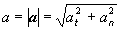                                                                                                          (2.1.25)

 

 Význam jednotlivých zložiek zrýchlenia je následovný:

·  tangenciálne zrýchlenie spôsobuje zmenu veľkosti rýchlosti,

·     normálové zrýchlenie (zrýchlenie dostredivé) spôsobuje zmenu smeru vektora  rýchlosti.

 

 

Poznámka: Postupy pri odvodzovaní rôznych fyzikálnych vzťahov môžu  byť rôzne.  Študent si môže vybrať a  naštudovať pre neho zrozumiteľnejší spôsob. Z tohto dôvodu ponúkame i  druhý   spôsob odvodenia vzťahu  pre normálové zrýchlenie.