2.2.3 Výpočet
ťažiska tuhého telesa
Každé bežné teleso sa skladá z obrovského množstva atómov, takže už nie je tvorené navzájom oddelenými časťami, ale infinitezimálne malými elementami o hmotnostiach dm. Teleso uvažujeme ako objekt so spojito rozloženou hmotnosťou. Všetky elementy telesa majú tiaž. Preto je dokonale tuhé teleso pod pôsobením nekonečného množstva príťažlivých síl. Všetky tieto sily možno nahradiť jednou silou. Bod pôsobenia tejto výslednej sily sa nazýva ťažisko . Súradnice ťažiska telesa získame, ak v rovniciach (2.2.3) pre ťažisko sústavy hmotných bodov súčty nahradíme integrálmi. Polohový vektor ťažiska rT telesa určuje vektorová rovnica
(2.2.6)
kde r je polohový vektor vybraného elementu dm vo zvolenej vzťažnej sústave a m je hmotnosť celého telesa. Súradnice ťažiska sú definované vzťahmi
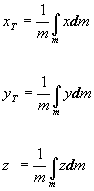(2.2.7)
Pri spojitom homogénnom rozložení hmotnosti v celom objeme telesa, hustotu telesa r s celkovou hmotnosťou m a celkovým objemom V vyjadríme vzťahom
(2.2.8)
odkiaľ pre element telesa dm, pri zvážení homogénnosti telesa (r = konšt.), platí
(2.2.9)
Pre telesá s nerovnomerne rozloženou hmotnosťou možno hmotnosť vyjadriť vzťahom
(2.2.10)
Ak nahradíme hmotnostný element v rovnici (2.2.7) vzťahom (2.2.9) , súradnice ťažiska možno vyjadriť pomocou objemových elementov vzťahmi
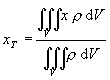
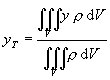
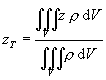(2.2.11)
Integráciu uskutočňujeme cez celý objem telesa V. Mnohé telesá vykazujú určitú geometrickú symetriu, ktorá môže byť napríklad stredová, osová alebo rovinná. Určiť polohu ťažiska homogénneho telesa nám uľahčuje práve jeho symetria. Ak je teleso symetrické podľa stredu, ťažisko sa nachádza v strede symetrie:
· Ťažisko homogénneho kvádra (obr. 2.2.2 ) sa nachádza v priesečníku telesových uhlopriečok.
· Ťažisko plnej homogénnej gule sa nachádza v strede gule.
· Ťažisko homogénnej rovinnej dosky tvaru rovnoramenného trojuholníka sa nachádza v priesečnici ťažníc.
· Ťažisko homogénneho valca sa nachádza na osi valca v polovici jeho výšky.
Ťažisko v niektorých prípadoch môže ležať i mimo telesa. Ťažisko zlatej obrúčky leží mimo prsteňa, v strede symetrie.
Ťažisko homogénneho telesa, ktoré je symetrické podľa určitej roviny tak, že ho delí na dve zrkadlové časti, leží v tejto rovine. (Napr. kokosový orech , slivka alebo banán).
V prípade, že chceme určiť ťažisko rovinného, resp. dĺžkového útvaru pomocou rovníc (2.2.7), integráciu cez hmotnosť skúmaného útvaru možno nahradiť integráciou cez plochu S resp. dĺžku l uvažovaného útvaru. Namiesto objemovej hustoty r telesa určenej rovnicou (2.2.8) možno zaviesť plošnú hustotu s resp. dĺžkovú hustotu l , pomocou ktorých vyjadríme hmotnostný element nasledovným spôsobom:
· Pre homogénny rovinný útvar s hmotnosťou m a plochou S, zanedbateľnej hrúbky h, vzťah (2.2.9) možno upraviť
(2.2.12)
kde sme zaviedli element plochy dS a plošnú hustotu rovinného útvaru s vzťahom
(2.2.13)
Ak dosadíme vzťah (2.2.12) do (2.2.11) pre ťažisko homogénneho rovinného útvaru ležiaceho v rovine xy dostávame vzťahy
(2.2.14)
Poznámka: Je nevyhnutné si uvedomiť, že v prípade nehomogénneho rovinného útvaru nemôžeme v rovniciach (2.2.14) plošnú hustotu vyňať pred integrál a celkovú hmotnosť musíme nahradiť integrálom cez hmotnostné elementy, určené rovnicou (2.2.12).
· Pre homogénny dĺžkový útvar s hmotnosťou m a dĺžkou l, zanedbateľného prierezu S , vzťah (2.2.9) možno upraviť
(2.2.15)
kde sme zaviedli element dĺžky dl a dĺžkovú hustotu l dĺžkového (lineárneho) homogénneho útvaru ( napr. drôtu) vzťahom
(2.2.16)
Po jeho dosadení do (2.2.11) pre ťažisko homogénneho dĺžkového útvaru, umiestneného do smeru osi x, dostávame vzťah
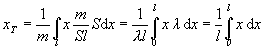(2.2.17)
Využitie symetrie pri určovaní polohy ťažiska a uvedených vzorcov si demonštrujeme na príkladoch:
Príklad 2.2.2
Z homogénneho
kartónu vystrihneme dva útvary
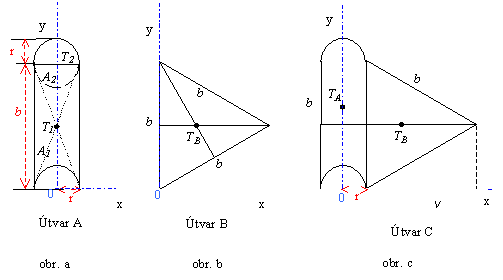
A a B, zobrazené na obrázku. Určite: a) polohu ťažiska
jednotlivých útvarov A a B, b) polohu ťažiska výsledného útvaru,
ktorý vznikne spojením, A a B, tak že útvary priložíme k sebe
stranami s veľkosťou b.
Riešenie:
Určíme si najprv polohu ťažiska útvaru A , resp. B. vo zvolenej súradnicovej
sústave. Jednou z možností voľby súradnicovej sústavy ukazuje obr. a. Y-ova os spadá do osi útvaru A, takže x-ová súradnica ťažiska útvaru
A leží na tejto osi, t.j. xTA =
O. Z obr. vidieť, že útvar A sa
skladá z dvoch častí - A1 obdĺžnika so stranami 2r a b,
ktorý ma na obidvoch koncoch vyrezaný polkruh o polomere r, a A2 kruh s polomerom r. Každý z útvarov A1 a A2
možno nahradiť hmotným stredom,
v ktorom je sústredená celková hmotnosť m1 , resp. m2.
Zo symetrie zvolených útvarov pre polohu ťažiska vo zvolenej súradnicovej
sústave platí:
xT1
= xT2 = 0 yT1 = b/2 yT2 = b
m1
= s
S1 a
m2 = s S2,
kde S1 = 2r b - pr2 , S2 = pr2. Pretože obidve x-ové súradnice sú nulové, bude aj x-ová súradnica útvaru A nulová, t.j. xTA = 0. Pre y-ovú súradnicu platí rovnica (2.2.3). Po dosadení získame
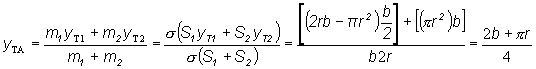
Určíme polohu ťažiska rovnostranného trojuholníka, ktorý si orientujeme tak, ako ho priložíme k útvaru A, ako je znázornené na obr. b, vzhľadom na súradnicovú os y prechádzajúcou stranou b. Ťažisko bude ležať v jednej tretine výšky v od základne , t.j:
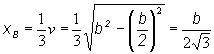
b) Určime
ťažisko útvaru vzniknutého spojením útvarov A a B pri orientácii znázornenej na obr. c,
vzhľadom na súradnicovú sústavu
prechádzajúcu osou útvaru A, v ktorej
súradnice 
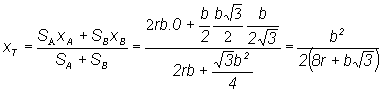
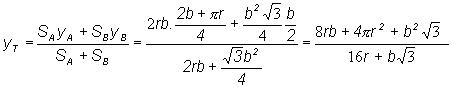
Príklad
2.2.3
Nájdite polohu ťažiska tenkej homogénnej hadičky (zanedbateľného prierezu) ohnutej do tvaru
polkružnice s polomerom R.
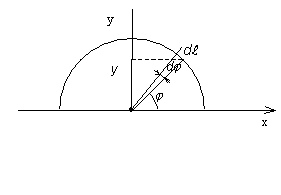
Riešenie:
Vo zvolenej súradnicovej sústave (obr. 1) ťažisko dĺžkového útvaru bude vzhľadom na symetriu podľa osi y, ležať na
tejto osi, t.j. xT =0.
Y-ovú súradnicu ťažiska určíme z rovnice (2.2.7)
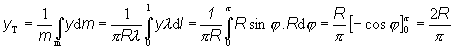
Pri výpočte sme vyjadrili y-súradnicu vybratého
elementu v polárnych súradniciach a
využili prepis dĺžkového elementu do polárnych súradníc, dl = R dj. Ťažisko
má súradnice:
a leží mimo daného objektu.
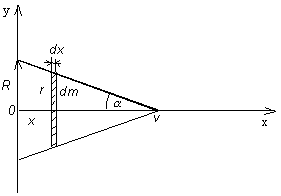
Príklad 2.2.4
Vypočítajte
polohu ťažiska homogénneho rotačného kužeľa s polomerom postavy R a výškou v
Riešenie: T [x, 0,
0]
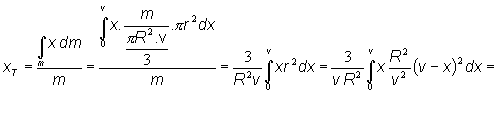
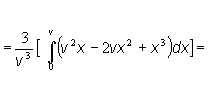
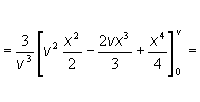
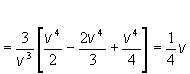
Kontrolné otázky k časti 2.2
1.
Definujte sústavu
hmotných bodov.
2.
Definujte homogénne
dokonale tuhé teleso.
3.
Matematicky
vyjadrite hmotnostný element lineárneho, plošného a objemového útvaru.
4.
Definujte
a matematicky zapíšte vzťahy pre objemovú hustotu r, plošnú hustotu s a lineárnu hustotu l.
5.
Určite koľko stupňov
voľnosti má hmotný bod pohybujúci sa na guľovej ploche. Uveďte príklad takéhoto pohybu.
6.
Ak sa vlak pohybuje,
existujú na tomto vlaku body, ktoré sa nepohybujú v smere pohybu vlaku?
7.
Definujte hmotný
stred sústavy hmotných bodov a tuhého
telesa.
8.
Určite polohu
hmotného stredu sústavy troch častíc s rovnakými
hmotnosťami, umiestnenými vo vrcholoch rovnostranného trojuholníka so stranou a.
9.
Vysvetlite súvis
symetrie telesa s polohou jeho ťažiska. Uveďte príklady.
10.
Môže sa nachádzať
ťažisko homogénneho telesa mimo
telesa? Ak áno, uveďte príklady.
11.
Nájdite polohu
ťažiska homogénnej kruhovej dosky tvaru štvrťkružnice s polomerom R.
12.
Závisí poloha
ťažiska sústavy hmotných bodov od zvolenej
súradnicovej sústavy?
13. Zvážte koľko existuje možností vytvorenia výsledného objektu zložením dvoch objektov A a B z príkladu 2.2.2. Zmení sa poloha ťažiska?
14. Definujte všeobecný pohyb tuhého telesa.
15. Kedy hovoríme, že teleso koná translačný pohyb? Čo možno povedať o rýchlostiach ľubovolných dvoch bodov telesa?
16. Určite aké dva typy rotácii môže vykonávať tuhé teleso?
17. Matematicky vyjadrite súvis medzi obvodovou a uhlovou rýchlosťou bodov telesa.
18. Kedy používame pravidlo pravej ruky? Uveďte príklad.
19. Určite aký smer má vektor uhlovej rýchlosti pri rotácii tuhého telesa okolo pevnej osi.
20. Určite aký smer má vektor uhlovej rýchlosti pri pohybe tuhého telesa okolo pevného bodu.
21. Určite koľko stupňov voľnosti má rotujúce teleso okolo pevnej osi. Uveďte príklad.
22.
Akú krivku opisuje
ťažisko skokanky z veže počas pádu do bazénu?
23. Zmení sa krivka, ktorú opisuje ťažisko skokanky z veže, ak počiatočné podmienky boli rovnaké a skokanka vykonala vo vzduchu počas pádu do bazénu salto?