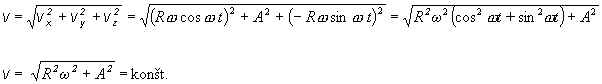2.1.3 Krivočiary pohyb
Krivočiary pohyb je charakterizovaný tým, že trajektória, ktorú opisuje hmotný bod je ľubovolná krivka. Ak časová závislosť polohového vektora sa mení podľa rovnice
r = r (x, y, z, t) (2.1.52)
hovoríme
o pohybe v priestore a musíme
uvažovať vektorovú rovnicu (2.1.7),
alebo parametrické rovnice (2.1.6), kde parametrom je premenná čas t. Tvar krivky, po ktorej sa pohybuje hmotný
bod, určený parametrickými rovnicami (2.1.6), určíme vylúčením parametra t
z parametrických rovníc, čím získame všeobecnú rovnicu dráhy.
Ak koncový bod polohového vektora r hmotného bodu sa v každom časovom okamihu nachádza v tej istej rovine, hovoríme o pohybe v rovine. V prípade , že aj začiatok súradnicovej sústavy, do ktorej je umiestnený začiatok polohového vektora r leží v tejto rovine pohybu, polohový vektor r ostáva vždy v tej istej rovine. Ako príklad rovinného pohybu možno uviesť pohyb stoličky, ktorú ťaháme po zemi (všetky nohy pri pohybe ostávajú na podlahe), alebo pohyb knihy po stole.
Na určenie pohybu v rovine úplné stačí, ak sú známe časové závislosti
dvoch jeho súradníc v danej rovine. Ak časová závislosť polohového
vektora sa mení v závislosti len
na súradniciach x a y, podľa rovnice
r = r (x, y, t)
hmotný bod, resp. teleso koná pohyb v rovine xy. Najjednoduchším krivočiarym pohybom je pohyb po kružnici, ktorému vzhľadom na závažnosť, venujeme pozornosť v samostatnej časti.
Krivočiary pohyb, podobne ako pri priamočiarom pohybe, delíme
z hľadiska rýchlosti pohybujúceho sa bodu na pohyb rovnomerný a nerovnomerný.
· Rovnomerný krivočiary pohyb
Ak vektor rýchlosti hmotného bodu
je konštantný len čo do veľkosti ( v = v0
= konšt.) znamená to, že sa mení jeho smer, vtedy hovoríme o rovnomernom krivočiarom pohybe.
Musíme si uvedomiť, že pri rovnomernom pohybe krivočiarom, celkové zrýchlenie
nie je nulové. Odvodenie tejto skutočnosti si ukážeme pri rovnomernom pohybe po
kružnici.
· Nerovnomerný krivočiary pohyb
Nech vektor zrýchlenia sa istým spôsobom s časom mení, a jeho zmena je určená predpisom a = a (t); v tomto prípade hovoríme o nerovnomernom krivočiarom pohybe hmotného bodu.
Ak vektor
zrýchlenia je konštantný čo do veľkosti (a = konšt.),
hovoríme o rovnomerne zrýchlenom
krivočiarom pohybe
Ak chceme určiť dĺžku dráhy resp. krivku v priestore, ktorú opisuje koncový bod polohového vektora r, ktorý sa pohybuje tak, že vektor zrýchlenia je určený funkčnou závislosťou a = a (t), postup je obdobný s predchádzajúcim prípadom po priamke, s tým rozdielom, že vzťahy definujúce zrýchlenie (2.1.17), rýchlosť (2.1.10) a časovú závislosť zrýchlenia a = a (t), musíme uvažovať ako vektory so zložkami a = [ax,ay,az], v = [vx,vy,vz] a r = [x,y,z,]. Vektorové rovnice, určujúce zrýchlenie (2.1.17) a rýchlosť (2.1.10) prejdú každá na tri skalárne rovnice, takže dostávame systém nasledovných rovníc (2.1.53)
ax = a1(t) ay = a2(t) az = a3(t)
![]() ,
, ![]()
![]() (2.1.53)
(2.1.53)
![]()
![]()
![]()
Ak sa jedná o pohyb rovinný uvažujeme len príslušné dve zložky, podľa toho, v ktorej rovine sa pohyb koná. Ich riešenie je obdobné, ako pre rovnice vystupujúce pre priamočiary pohyb. Postup si ukážeme na nasledovnom príklade.
___________________________________________
Príklad:
2.1.9 Časová
závislosť pohybu hmotného bodu je určená parametrickými rovnicami
x = k1,
y = k2t + k3t3,
kde k1, k2 a k3 sú konštanty.
Rozhodnite, aký pohyb koná hmotný bod a určite rýchlosť a
zrýchlenie hmotného bodu v základných jednotkách sústavy SI a) na konci
tretej sekundy pohybu, b) na
začiatku jedenástej sekundy pohybu, ak
k1 = 3 mm, k2 =
10 cm.s-1, k3 =
500 mm.s-3.
Riešenie:
Uvedomíme si zadané veličiny a presvedčíme sa, či tieto
veličiny sú v základných jednotkách SI sústavy. Vypíšeme si ich a nakoľko
nie sú v základných jednotkách SI,
premeníme ich:
k1 = 3 mm = 3.10-3 m
k2 = 10 cm. s-1
=10. 10-2 m.s-1 =
10-1 m.s-1
k3 = 500 mm.s-3
= 500.10-6 m.s-3 =
5.10-4 m.s-3
a)
t1 = 3 s, v1 = ? , a1
= ?
b) t2
= 10 s, v2 = ? , a 2
= ?
Pohyb hmotného bodu je daný
dvoma rovnicami pre časovú závislosť polohového vektora r(t)
= [x (t), y(t) ] = [x, y],
takže sa jedná o pohyb v rovine xy.
Rýchlosť a zrýchlenie sú vektorové fyzikálne veličiny, musíme určiť aj ich veľkosť aj ich smer.
Napíšeme si základné vzťahy pre hľadané
veličiny v = [vx,
vy ]
a a = [ax,
ay
], kde
![]() ,
,
![]()
![]() .
.
![]()
![]()
![]() .
.
Smer vektorov v a a určíme
z trigonometrickej funkcie
cos a
.
![]()
Do základných vzťahov dosadíme zadané parametrické rovnice a vykonáme naznačené matematické operácie:
![]()
![]()
![]()
![]()
![]()
Pre
veľkosť a smer rýchlosti po číselnom
dosadení dostávame v prípade:
a) v(t1) =
10-1 m.s-1 + 3. 5.10-4 m.s-3(3
s)2 = ( 0,1 +0,0135) m.s-1 =
0,1135 m.s-1
Pozn:
Pre určenie smeru možno zvoliť i inú trigonometrickú funkciu. Ak by sme si zvolili
![]()
vidíme,
že funkcia nie je definovaná, nakoľko x-ová
zložka rýchlosti je nulová. Vieme teda, že pohyb hmotného bodu sa uskutočňuje
v smere odklonu od x-ovej
osi určenom uhlom a
= 90 o, čo odpovedá smeru osi
y .
b) v
(t2) = 10-1 m.s-1 + 3. 5.10-4
m.s-3(10 s)2 = (
0,1 +0,15) m.s-1 = 0,25 m.s-1
Pre
zadaný prípad, obdobne smer vektora
rýchlosti je v smere osi y. Zrýchlenie
určíme na základe už uvedených vzťahov
![]() kde
kde 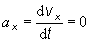
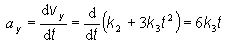
![]()
Pre
veľkosť a smer zrýchlenia po číselnom dosadení dostávame
v prípade
a) a
(t1) = 6 k3 t1
= 6. 5.10-4 m.s-3(3
s) = 0,009 m.s-2
a (t1) = 0,009 j [m.s-2]
b) ![]()
a (t2) = 0,3 j [m.s-2
]
čo
znamená, že aj vektor rýchlosti a
leží v smere súradnicovej osi y .
Odpoveď:
Hmotný bod pohybujúci sa podľa parametrických rovníc v zadaní vykonáva
nerovnomerný priamočiary pohyb v smere jednotkového vektora j s veľkosťou rýchlosti v = 0,235 m.s-1 a veľkosťou zrýchlenia
a = 0,09
m.s-2 na konci tretej minúty, resp.
v
= 2,5 m.s-1 a a = 0,3 m.s-2 na začiatku jedenástej
sekundy.
Príklad 2.1.10 Mucha
lieta tak, že jej súradnice závisia od času podľa rovníc: x = R
sin wt
, y = At,
z
= R cos wt,
kde R, w a A sú konštanty. Rozhodnite,
o aký pohyb sa jedná a určite vektor rýchlosti a vektor zrýchlenia jej
pohybu, ako i veľkosť zložky tangenciálneho a normálového zrýchlenia.
Riešenie:
Zo zadania troch parametrických rovníc vieme povedať, že mucha vykonáva
priestorový pohyb. Dráha je skrutkovnica v smere osi y, určená
parametrickými rovnicami
x = R sin w t
y = At
z = R cos
w t
Vektor
rýchlosti určíme zo vzťahu
![]()
![]()
|
|
Vektor
zrýchlenia určíme ako deriváciu vektora rýchlosti
![]()
![]()
![]()
![]()
Príklad 2.1.11
Zrnko
prachu sa pohybuje po skrutkovnici tak,
že jeho polohový vektor r v čase t je určený rovnicou (1):
r = iR cos wt +jR sinwt + kvt ,
kde R, w a v sú kladné
konštanty. Akú dlhú dráhu s prejde
zrnko za časový interval Dt = t
– t0 , keď v čase t0 = 0 sa nachádzalo
zrnko v začiatku súradnicového systému, t.j r0 = 0
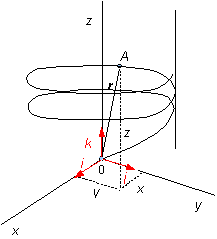
Riešenie: Elementárna dĺžka dráhy ds, ktorú zrnko prebehne je daná rovnicou
![]() (2)
(2)
pričom
z rovnice (1) platí:
x
= R cos wt, y
= R sin wt, z
= n t
odkiaľ
pre diferenciály platí
dx = -R w sin w t dt, dy = Rw cos w t dt, dz = v dt (3)
Po
dosadení rovníc (3) do rovnice (2)
dostaneme:
![]()
![]() (4)
(4)
Integrovaním
rovnice (4) dostaneme celkovú
dĺžka dráha Ds
, ktorú zrnko prešlo za časový interval D t = t
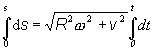
![]()
Kontrolné otázky k časti 2.1.3
1. Charakterizujte
krivočiary pohyb.
2. Uveďte
niektoré špeciálne prípady krivočiareho
pohybu.
3. Aký
smer má rýchlosť pri krivočiarom pohybe?
4. Do
akých zložiek rozkladáme vektor zrýchlenia pri krivočiarom pohybe
v rovine?
5. Ak sa teleso
pohybuje s konštantným celkovým
zrýchlením rozhodnite, či môže mať
jeho dráha tvar určenú ktoroukoľvek
z nasledovných kriviek :a) priamka
b) kružnica
c) špirála d) ľubovolný tvar.
6. Môže
byť vektor rýchlosti konštantný pri krivočiarom pohybe?
7. Ak
častica koná rovnomerný krivočiary pohyb, aký smer má vektor rýchlosti?
8. Vyjadrite
dĺžku ubehnutej dráhy hmotného bodu, ktorý sa pohybuje krivočiarym pohybom a)
v rovine, b) v priestore.
9. Ak
všetky body telesa sa v rovnakých časových intervaloch posunú
o rovnakú vzdialenosť v tom istom smere, aký pohyb skúmané teleso koná?
10. Ovplyvňujú
sa navzájom jednotlivé zložky popisujúce priestorový pohyb?
11. Môže
sa častica pohybovať po špirále, ak jej normálové zrýchlenie je nulové?
12. Aký
pohyb koná teleso vrhnuté z výšky h vodorovným
smerom s nenulovou počiatočnou
rýchlosťou?
13. Čo
je grafom závislosti dráhy od času telesa vrhnutého z výšky h vodorovným smerom s nenulovou počiatočnou rýchlosťou?
14. Akým
smerom je orientovaný vektor okamžitej rýchlosti vzhľadom na trajektóriu?
15. Napíšte
matematické vyjadrenie závislosti z- ovej zložky rovnice trajektórie, ak
častica koná pohyb po závitnici
s osou spadajúcou do osi z.
Nakreslite obrázok.
16. Vysvetlite,
čo je oskulačná rovina a oskulačná kružnica.
17. Kedy
sa častica, schopná otáčať sa okolo nehybnej osi, otáča s uhlovým zrýchlením? Formulujte aj matematický vzťah.