·       Uhlová rýchlosť a uhlové zrýchlenie

            Skúmame pohyb hmotného bodu po krivke K znázornenej na obrázku 2.1.7

 

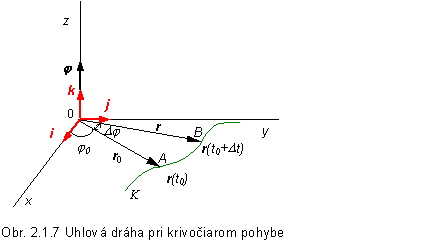
            Vidíme, že trajektória pohybu leží v rovine xy a  jedná sa o krivočiary pohyb v rovine xy. Hmotný bod na začiatku skúmania pohybu, t.j. v čase  t0 , sa nachádza v bode A určeným polohovým vektorom r0  a v čase t0 +Dt v bode B, určeným  polohovým vektorom r . Z obrázku vidíme tiež, že vo zvolenom prípade veľkosti vektorov r0 a r  sú rôzne. To znamená, že ilustrovaný pohyb prezentuje  všeobecný prípad, kedy sa pri pohybe môže meniť veľkosť i smer polohových vektorov hmotného bodu v jednotlivých časových okamihoch. Pre zjednodušenie  budeme uvažovať taký pohyb, pri ktorom veľkosť polohových vektorov sa nemení a pohyb prebieha v rovine. Hovoríme o pohybe po kružnici.

V tomto zjednodušenom prípade nás bude  zaujímať, ako sa mení uhol, ktorý vytvára malá zmena polohového vektora pohybujúceho sa hmotného bodu vzhľadom na pevne zvolený počiatok  0 a smer ( napr. x).

            Nech hmotný bod za časový interval Dt opíše uhol Dj , ktorý zvierajú polohové vektory r0 a r . Zmena uhlu Dj  pripadajúca na jednotku času definuje  veličinu, ktorú nazývame stredná uhlová rýchlosť ws

 

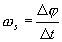                                                                                                                         (2.1.26)

 

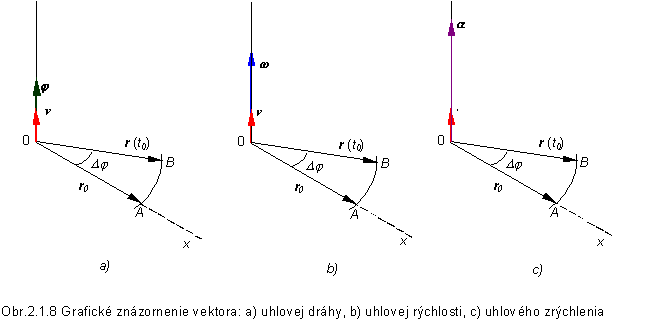
            Je výhodné  uhlu Dj , vytvorenému zovretím dvoch málo odlišných  smerov, t.j. uhlu medzi polohovými vektormi r a r0 , priradiť  vektor uhlovej dráhy Dj 

( obr. 2.1.8 a) definovaný rovnicou

 

Dj  = Dj n                                                                                                                       (2.1.27)

 

nasledovne:

·     vektor Dj má smer  jednotkového vektora n  a je  kolmý na rovinu, v ktorej ležia polohové vektory r a r0 ,

·     vektor Dj   je orientovaný na tú stranu, z ktorej vidíme stotožnenie polohového vektora r0  do smeru polohového vektora r po kratšej uhlovej dráhe v zmysle  proti pohybu   hodinových ručičiek,

·     absolútna hodnota vektora uhlovej dráhy Dj  sa  rovná veľkosti uhla zovretého obidvoma smermi.

 

Uhol, aký opíše  sprievodič za jednotku času, udáva veličina uhlová rýchlosť. V limitnom prípade Dt®0  podiel určený rovnicou (2.1.28) určuje okamžitú uhlovú rýchlosť, resp. uhlovú rýchlosťw ( obr.2.1.8 b)

 

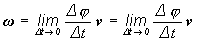
                                                                                      (2.1.28)

 

ktorú možno vyjadriť ako deriváciu uhlovej rýchlosti podľa času vzťahom

 

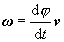                                                                                                                           (2.1.29)

 

Na základe definičného vzťahu pre uhlovou rýchlosť (2.1.29), možno veľkosť  uhlovej dráhy, opísanej za časový interval

t - t0 , vyjadriť rovnicou

 

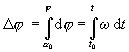
                                                                                                       (2.1.30)

 

kde j0 udáva uhol, ktorý zviera polohový vektor r0  hmotného bodu  A  na začiatku skúmania so zvoleným smerom. Obvykle je výhodné zvoliť taký súradnicový systém, aby ja bolo rovné nule.                                 

            Vektorová veličina  uhlové zrýchlenie a  je definovaná ako časová derivácia uhlovej rýchlosti

 

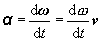                                                                                                                (2.1.31)

 

 a možno ju vyjadriť i pomocou uhlovej dráhy nasledovne:

 

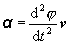                                                                                                                              (2.1.32)

 

resp. ako každý vektor cez jeho  veľkosť  a  a smer určeným jednotkovým vektorom n, kolmým na rovinu, v ktorej sa pohyb odohráva (obr. 2.1.8 c)

 

a  = a n                                                                                                                            (2.1.33)

 

Jednotkou uhlovej rýchlosti w  je s-1 a uhlového zrýchlenia a  je  s-2.

 

Kontrolné otázky k časti 2.1.1

 

1.     Čím sa zaoberá mechanika hmotného bodu a telesa?

2.     Aké je základné rozdelenie mechaniky hmotného bodu a telesa?

3.     Ktorá časť mechaniky neskúma príčiny pohybu?

4.     Ktorá časť mechaniky sa zaoberá len opisom pohybu?

5.     Čo je predmetom štúdia kinematiky?

6.     Čo je predmetom štúdia dynamiky?

7.     Akou rýchlosťou sa môže pohybovať hmotný bod, resp. teleso, aby sme jeho pohyb vyšetrovali pomocou klasickej mechaniky?

8.     V akých prípadoch pohyb musíme vyšetrovať pomocou relativistickej mechaniky?

9.     Ktorá časť mechaniky sa zaoberá vyšetrovaním zákonitostí v oblasti mikrosveta?

10.  Ktorá časť mechaniky sa zaoberá podstatou pohybu  a  príčinou vzniku pohybov?

11.  Definujte pojem vzťažná sústava.

12.  Definujte pojem hmotný bod a uveďte príklady, kedy môžeme teleso považovať za hmotný bod.

13.  Aké základné dva druhy mechanického pohybu rozlišujeme?

14.  V akých vzťažných sústavách najčastejšie vyšetrujeme pohyb?

15.  Definujte pojem polohový vektor hmotného bodu a napíšte jeho matematické vyjadrenie. Vysvetlite význam jednotlivých veličín .

16.  Aké fyzikálne veličiny definujú polohu hmotného bodu v sférickej súradnicovej sústave. Vysvetlite ich význam.

17.  Napíšte rovnice, ktoré určujú súvis medzi súradnicami hmotného bodu v karteziánskej súradnicovej sústave a v  sférickej súradnicovej sústave?

18.  Ako určíme veľkosť polohového vektora hmotného bodu?

19.  Napíšte všeobecné analytické vyjadrenie polohy hmotného bodu v priestore.

20.  Vysvetlite, čo určujú smerové kosínusy polohového vektora hmotného bodu?

21.  Napíšte základné kinematické veličiny a ich matematické vyjadrenie.

22.  Definujte okamžitú rýchlosť hmotného bodu a vysvetlite rozdiel medzi strednou a okamžitou rýchlosťou. Sú v niektorom prípade tieto veličiny rovnaké? Ak áno, napíšte v ktorom.

23.  Napíšte vzťah pre smerový uhol, ktorý zviera vektor rýchlosti hmotného bodu s osou x, resp. y , z  karteziánskej súradnicovej sústavy, ak poznáte všetky zložky vektora  rýchlosti.

24.  Určite veľkosť vektora rýchlosti, ak poznáte jeho zložky rýchlosti a určite smer vektora    rýchlosti.

25.  Akú polohu zaujíma vektor rýchlosti k trajektórii pohybu hmotného bodu?

26.  Vyjadrite jednotkový vektor v smere dotyčnice k trajektórii,  ak poznáte vektor rýchlosti.

27.  Definujte pojem  okamžité zrýchlenie hmotného bodu. Napíšte matematický vzťah, určujúci veľkosť zrýchlenia.

28.  Nakreslite si ľubovolnú trajektóriu hmotného bodu a pre Vami zvolený prípad určite smer vektora zrýchlenia.

29.  Za predpokladu, že poznáte vektor rýchlosti a vektor zrýchlenia, vyjadrite jednotkový vektor v smere normály ku dráhe hmotného bodu.

30.  V sústave SI napíšte jednotku rýchlosti a jednotku zrýchlenia.

31.  Do akých dvoch smerov je výhodné (resp. obvyklé) rozkladať vektor zrýchlenia hmotného bodu?

32.  Vysvetlite fyzikálny význam   tangenciálnej zložky zrýchlenia.

33.  Vysvetlite fyzikálny význam normálového  zrýchlenia.

34.  Definujte pojmy uhlová dráha, uhlová rýchlosť a uhlové zrýchlenie.

35.  Napíšte matematické vzťahy, vyjadrujúce súvislosť medzi uhlovou dráhou, uhlovou rýchlosťou a  uhlovým  zrýchlením.

36.  Možno určiť polomer krivosti trajektórie hmotného bodu v danom okamihu a mieste, ak poznáte vektor rýchlosti a vektor zrýchlenia v danom okamžiku a mieste? Ak áno, napíšte matematické vyjadrenie polomeru  krivosti v závislosti od udaných veličín.

37.  V sústave SI napíšte jednotku uhlovej rýchlosti a uhlového zrýchlenia.