2.1.6 Zložený pohyb

Pozorujme pohyb napríklad kotúľajúcej sa gulôčky rovnomernou rýchlosťou vo vagóne.  Zmení sa pohyb guľôčky z pohľadu výpravcu stojaceho na nástupišti,  resp. z pohľadu cestujúceho sediaceho vo vagóne,  ak sa vagón začne pohybovať rovnomerne zrýchlene? Skúste si odpovedať na otázku zo skúsenosti.

Ak chceme fundovane odpovedať na obidve časti otázky, je nevyhnutné si uvedomiť,  vzhľadom na ktorý pevný bod chceme pohyb skúmať Ak nás zaujíma pohyb gulôčky  v pohybujúcom sa vagóne vzhľadom na výpravcu stojaceho na nástupišti,  hovoríme, že skúmame zložený pohyb. Ako ďalší príklad zloženého pohybu možno uviesť pohyb dažďových kvapiek na oknách pohybujúceho sa auta  a iné.

Vo všeobecnosti možno definovať zložený pohyb nasledovne: Uvažujme vzťažný bod O (resp. teleso v priestore), ktorý sa nepohybuje a vzťažný bod O´ (resp. teleso v priestore), ktorý sa voči pevnému bodu O pohybuje. Ak je daný pohyb hmotného bodu (telesa) A voči vzťažnému bodu O´ a pohyb vzťažného bodu O´ vzhľadom na O, vieme určiť priamo pohyb hmotného bodu A vzhľadom na vzťažný bod O. Pohyb vzťažného bodu A vzhľadom na vzťažný bod O nazývame pohybom zloženým.

 

 

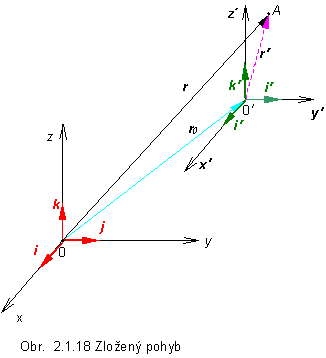
Skúmame pohyb hmotného bodu A vzhľadom na obidve sústavy, tj. určíme jeho vektor rýchlosti a vektor zrýchlenia (obr. 2.1.19). Nech:

r   je polohový vektor bodu A  v karteziánskej vzťažnej sústavu pevne spojenej s počiatkom      

    v bode   O,  ktorú označíme S [O, x, y ,z ];

r´ je polohový vektor bodu A v karteziánskej  súradnicovej sústave pevne spojenej s počiatkom

    v bode O´ , ktorú označíme S´ [O´, x´, y´, z´ ];

r_o je polohový vektor bodu O´ vzhľadom na počiatok karteziánskej súradnicovej sústavy pevne

    spojenej  s počiatkom  v bode O, tj. polohový vektor bodu O´  vzhľadom na O.

Nech sa sústava S´ [O´, x´, y´, z´ ]  pohybuje voči pevnej sústave S [O, x ,y ,z ].  Vieme, že každý pohyb vo všeobecnosti možno zložiť z kombinácie translačného a rotačného pohybu. Teda dva  krajné  prípady, s ktorými sa pri skúmaní zloženého pohybu stretávame najčastejšie,  sú práve:

 

I.    Sústava S´ [O´, x´, y´, z´ ] koná voči S [O, x, y, z ] len translačný (posuvný) pohyb. Pri tomto  pohybe:

·     sa mení jej polohový vektor r_o = r_o(t),  resp. možno povedať, že sa mení poloha bodu O´ voči bodu O;.

·     vzájomná orientácia osí sa nemení ;  

·     poloha  skúmaného bodu  A  sa vzhľadom na sústavu S´ [O´, x´, y´, z¢ ] nebude meniť, t.j.  r´ = konšt. (čo do veľkosti i smeru ).

·     derivácia vektora r´ podľa času  vzhľadom na sústavu S´ [O´, x´, y´ ,z´ ] je nulová.

 

II. Sústava S´ [O´, x´, y´ ,z´ ] koná voči S [O, x, y, z ] len rotačný pohyb okolo osi prechádzajúcej počiatkom O , t.j.  bod O´ je totožný s bodom O´  [ O º O´].  V tomto prípade:

·     poloha bodu O´  sa nemení vzhľadom na S  [O, x, y ,z ];

·     mení sa vzájomná orientácia osí obidvoch sústav;  

·     pre skúmaný hmotný bod  A  sa  jeho poloha vzhľadom na sústavu  S´ [O´, x´, y´, z´ ] nebude meniť, čo do veľkosti ani smeru t.j. r´ = konšt.;

·     poloha bodu A vzhľadom na sústavu S [O, x, y, z ]  sa mení tak, že bod A opisuje kružnicu so stredom v bode O s polomerom r´,  s uhlovou rýchlosťou w . To však  znamená, že vektor r´ nie je konštantný. Veľkosť vektora r´  sa nemení, ale mení sa jeho smer ;

·     derivácia vektora r´ podľa času  vzhľadom na sústavu S [O, x, y, z ] je rôzna od nuly ;

·     vektor  uhlovej  rýchlosti w  hmotného bodu A nezávisí od polohy bodu A;

 

Pri určovaní rýchlosti a zrýchlenia hmotného bodu A musíme zvážiť, vzhľadom na ktorú sústavu pohyb skúmame, pretože derivácia polohového vektora r´ v týchto sústavách nie je rovnaká, čo si  následne ukážeme:

Deriváciu polohového vektora r´  bodu  A vzhľadom na  pevnú  sústavu S [O, x, y, z ] v ďaľšom budeme nazývať absolútnou deriváciou a označovať (dr´/dt)_a

 Deriváciu polohového vektora r´  bodu  A vzhľadom na pohybujúcu sa sústavu S´ [O´, x´, y´, z´ ] v ďaľšom budeme nazývať relatívnou   a označovať (dr´/dt)_r .

 

·       Derivácia jednotkového vektora, ktorého veľkosť je konštantná, ale  smer sa mení. 

 

Skôr kým nájdeme vzťah medzi absolútnou a relatívnou deriváciou je nevyhnutné si odvodiť  vzťah pre deriváciu jednotkového vektora, ktorého veľkosť je konštantná, ale  smer sa mení. 

Ukázali sme si, ( príklad 2.1.12), že pre vektor rýchlosti v platí rovnica

 

 

Keďže  v  = dr/dt  , kde  r  možno zapísať  pomocou  jednotkového  vektora  r  ako  r  = rr.  Pre polohový vektor  r , ktorého  veľkosť ostáva konštantná  a mení  sa  len  smer  platí:

 

 

 

                                                                                                              (2.1.121)

 

Rovnica (2.1.121) určuje deriváciu jednotkového vektora r  podľa času, ak sa jeho smer mení.

 

 

 

·       Absolútna a relatívna derivácia

 

Vyjadrime si polohový vektor r´ v sútave S´ [O´, x´, y´, z´ ]

 

r´ =  x´i´ + y´j´ + z´k´                                                                                                  (2.1.122)

 

a vypočítajme jeho deriváciu vzhľadom na sústavu S´, ktorá sa voči pevnej otáča uhlovou rýchlosťou w. Derivácia r´  bude určenú vzťahom

 

                                                                                                 (2.1.123)

 

Počítajme deriváciu vektora r´ vzhľadom na sústavu S, ktorá je pevná

 

 

Po preskupení členov

 

 

a využití vzťahu pre deriváciu jednotkového vektora  (2.1.121)  dostaneme

 

                                                (2.1.124)

 

 

respektíve s využitím pojmov absolútnej  derivácie, t.j. derivácie voči sústave pevnej a pojmu derivácie relatívnej , t.j. derivácie voči sústave pohybujúcej sa,  dostávame

 

                                                                                     (2.1.125)

 

Tento vzťah platí nielen pre polohový vektor r´, ale i pre akýkoľvek iný vektor.

 

·       Rýchlosť hmotného bodu A vzhľadom na absolútnu sústavu

 

Odvoďme vzťah pre rýchlosť hmotného bodu A vzhľadom na absolútnu sústavu, v ktorej má hmotný bod A polohový vektor 

 

r  =  r₀  + r´

 

                                       (2.1.126)

 

v   =   v₀  + v´ + (w ´ r´)                                                                                           (2.1.127)

 

kde

·     v₀ je rýchlosť počiatku pohybujúcej sa sústavy, t.j. bodu O´ vzhľadom na počiatok pevnej sústavy, t.j. bod  O ;

·     v´ je rýchlosť hmotného bodu A vzhľadom na O ´ ;

·     w  je vektor uhlovej rýchlosti otáčajúcej sa sústavy (w ´ r´).

·     r´ je polohový vektor hmotného bodu v pohybujúcej sa sústave.

 

Vzťah pre absolútnu rýchlosť v  nám hovorí: Ak sa hmotný bod pohybuje v sústave, ktorá sa pohybuje súčasne translačným i rotačným pohybom, celková rýchlosť  v  hmotného bodu vzhľadom na pevnú sústavu S je daná vo všeobecnosti vektorovým súčtom troch vektorov,  vektora rýchlosti počiatku pohybujúcej sa sústavy v₀, vektora rýchlosti hmotného bodu v pohybujúcej sa sústave v´ a vektora určeného vektorovým súčinom (w ´ r´). [ Vektor (w ´ r´) je vektor  kolmý na rovinu určenú vektormi w  a  r´, orientovaný do tej polroviny, z ktorej vidím stotožnenie vektora  w  do smeru  vektora   r´ po kratšej uhlovej dráhe  proti smeru pohybu hodinových ručičiek.]

V prípade, že sústava koná  len  translačný  pohyb absolútna rýchlosť je daná vzťahom

 

v =   v₀  + v´                                                                                           (2.1.128)

 

V prípade, že sústava koná len rotačný pohyb,  absolútna rýchlosť je daná vzťahom

 

v   =   v₀  + (w ´ r´)                                                                                (2.1.129)

 

Pre rýchlosť hmotného bodu A vzhľadom na O´ možno písať

 

v´   = v  -  v₀  - (w ´ r´)                                                                                           (2.1.130)

 

 

• Zrýchlenie hmotného bodu A vzhľadom na absolútnu sústavu

 

Odvoďme vzťah pre zrýchlenie hmotného bodu A vzhľadom na absolútnu sústavu:

 

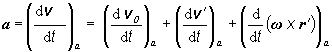                                               (2.1.131)

 

kde za rýchlosť dosadíme rovnicu (2.1.127)

 

 

Po vykonaní naznačených matematických úkonov s využitím vzťahu  (2.1.125), ktorý nám určuje súvislosť medzi absolútnou a relatívnou deriváciou ľubovolného vektora, a teda i vektorov v´, v₀ , w  a r´ dostávame

 

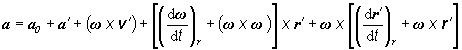
a    =  a₀  +  a´ +   (w ´ v´)  +  a ´  r´  + (w ´ v´) +  w   ´  (w ´ r´)

 

Poznámka: Pri úprave sme využili:

 

 

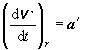
definíciu uhlového zrýchlenia  a skutočnosť,  že vektorový súčin toho istého vektora so sebou je vždy nulový, takže

 

 

 

t.j. absolútna a relatívna derivácia vektora uhlovej rýchlosti sú totožné.

 

Po preskupení členov a po úprave dostaneme výsledný vzťah pre absolútne zrýchlenie hmotného bodu A vzhľadom na absolútnu sústavu

 

a    =  a₀  +  a´ +  2 (w ´ v´)  + w   ´  (w ´ r´)  +  a ´  r´                                   (2.1.132)

 

v ktorom

·     vektor a₀  určuje  zrýchlenie počiatku pohybujúcej sa sústavy, t.j. bodu O´ vzhľadom na počiatok pevnej sústavy, t.j. bod  O ;

·     vektor a´  určuje zrýchlenie  hmotného bodu A vzhľadom na O´ ;

·     vektor 2 (w ´ v´) sa nazýva Coriolisovo zrýchlenie. Je to vektor, ktorý je kolmý na vektor uhlovej  rýchlosti w   i na vektor (relatívnej ) rýchlosti v´  ;

·     vektor w   ´  (w ´ r´)   je na okamžitú os otáčania kolmý a smeruje do tejto osi a predstavuje dostredivé zrýchlenie vzhľadom na pevnú  súradnicovú sústavu ;

·     vektor  (a x r´) je od nuly rôzny vtedy, keď uhlová rýchlosť otáčania w  nie je konštantná, ale sa mení s časom.

Vzťah  pre  absolútne  zrýchlenie a   hovorí:  Ak sa hmotný  bod pohybuje v sústave, ktorá sa pohybuje súčasne translačným i rotačným pohybom, celkové zrýchlenie a  hmotného bodu vzhľadom na pevnú sústavu S je dané vo všeobecnosti vektorovým súčtom piatich  vektorov:  vektora zrýchlenia  počiatku pohybujúcej sa sústavy a₀, vektora zrýchlenia (relatívneho) hmotného bodu v pohybujúcej sa sústave a´, Coriolisovho zrýchlenia (je to vektor kolmý na rovinu  určenú vektormi w  a v´ ), dostredivým zrýchlením,  a ak sústava rotuje nerovnomerným pohybom, tak i vektorom, kolmým na rovinu určeného vektorovým súčinom vektorov a a r´ .

 

V prípade, že sústava koná len translačný pohyb, absolútne zrýchlenie  je dané vzťahom

 

a    =  a₀  +  a´                                                                                                           (2.1.133)

 

V prípade, že sústava koná len rotačný pohyb  absolútna rýchlosť je daná vzťahom

 

a    = a´ +  2 (w ´ v´)  + w   ´  (w ´ r´)  +  a ´  r´                                                   (2.1.134)

 

 

Pre zrýchlenie  hmotného bodu A vzhľadom na O´ možno písať

 

 a´    = a  -  a₀ -  2 (w ´ v´)  - w   ´  (w ´ r´)  -  a ´  r´                                            (2.1.135)

 

Rozdiel medzi rovnicami pre absolútne zrýchlenie a a relatívne zrýchlenie a´ je v tom, že výraz w ´ (w ´ r´) predstavuje pre pozorovateľa v absolútnej sústave dostredivé zrýchlenie, kým pre pozorovateľa v pohybujúcej sa sústave viazaného na O´ zrýchlenie odstredivé.

________________________________

Príklad 2.1.16

Na gramofónovej doske, ktorá sa otáča okolo zvislej osi tak, že za pol minúty vykoná 60 otáčok, sa nachádza mravec, ktorý sa pohybuje rovnomernou rýchlosťou v´= 1 cm.s^-1. Určite rýchlosť a zrýchlenie pohybujúceho sa mravca vzhľadom na okolie ( gramofón) v čase t = 10 s , ak v okamžiku počiatku merania sa mravec nachádzal v strede dosky a pohybuje sa pozdĺž jej polomeru.

Riešenie:

 

f   = 60 ot /30 s = 2 ot.s^-1

v´ =  1 cm. s^-1 = 10^-2 m.s^-1

t₀  =  0 s

t₁ = 10 s

 

Gramafónová doska a po nej pohybujúci sa mravec možno považovať za pohyb v sústave S´, t.j.  v relatívnej sústave. Doska sa otáča vzhľadom na gramafón, pevne umiestnený v sústave S, t.j. v absolutnej sústave. Pohyb mravca vzhľadom na pevnú sústave považujeme za pohyb zložený. Pre rýchlosť v absolutnej sústave preto použijeme vzťah (2.1.127)

 

v   =   v₀  + v´ + (w ´ r´)

 

Nakoľko gramofón je umiestnený pevne, rýchlosť v₀ = 0 m.s^-1 a teda absolútna rýchlosť je určená pomocou v´ = konšt. a r´= v´t  vzťahom

 

v   =  v´ + (w ´ r´) = v´ + (w ´ v´t)

 

Je treba si uvedomiť, že zo zadania príkladu je žiadúce určiť vektor rýchlosti i zrýchlenia, ale to  znamená určiť ich veľkosť i smer.

Určime si jednotlivé vektory, ktoré vo východzom vzťahu vystupujú:

Vektor w je kolmý na rovinu dosky, v ktorej pohyb sa uskutočňuje a leží v osi otáčania, prechádzajúcej stredom dosky a je  teda  kolmý i na vektor rýchlosti v´, ktorý leží v rovine dosky . Preto pre  veľkosť vektora určeného vektorovým súčinom platí

 

½(w  ´ v´t) ½= ½w ½½ v´t ½sin 90 ⁰ = w v´t

 

Orientáciu  vektorov w  a  v´ si zvolíme  napríklad  nasledovne: w  = (0,0, w ) a v´ = ( v´, 0,0) .

( Poznámka: Voľba inej voľby súradnicového systému je samozrejme možná.)

Z vlastností vektorového súčinu  vieme, že smer vektora (w ´ v´t) je kolmý na rovinu určenú vektormi w  a  v´, a smeruje do polpriestoru s kladnou y-ovou osou,  nakoľko pri zvolenej súradnej sústave  - vektor  uhlovej rýchlosti spadajúci do z-tovej osi  a pohyb mravca v smere x-ovej osi,  platí

 

w ´ v´t =w k ´  v´t i = w v´t ( k ´ i) = w v´t j

 

Pre veľkosť absolutnej rýchlosti na základe sčitovania dvoch kolmých vektorov platí

 

 

Po číselnom dosadení

 

 

Smer vektora  rýchlosti v okamžiku t = 10 s možno určiť na základe goniometrických funkcií z obrázku, napríklad  pomocou uhlu odklonu a  od x-ovej osi, v smere ktorej ležal vektor rýchlosti v´ v okamžiku t₀ = 0 s

 

cos a  =       Þ  a  = arccos

 

Po číselnom dosadení

 

cos a = O, 007955  Þ a = 89 ⁰  30 ´

 

Pre absolútne zrýchlenie platí všeobecný vzťah (2.1.132)

 

a    = a´ +  2 (w ´ v´)  + w  ´ (w ´ r´)  +  a ´  r´

 

Relatívna sústava - gramofón sa nepohybuje a  platňa sa voči gramofónu otáča konštantnou uhlovou  rýchlosťou, takže a´ i a  sú nulové. Po zvážení počiatočných podmienok daných  príkladom, pre absolútne zrýchlenie dostávame

 

a  =  2 (w ´ v´)  + w  ´ (w ´ r´) 

 

Pri nami zvolenej súradnicovej sústave obdobne ako vyššie platí

 

w  ´ v´ = w k ´  v´ i = w v´ ( k ´ i) = w v´ j

 

w ´ (w ´ r´)  = w k ´ (w k ´ r´i) = w k ´ w r´(k ´ i) = w ²r´ k ´ j = w ²r´(-i)

 

Zrýchlenie w ´  (w ´ r´) je vektor kolmý na rovinu yz a znamienko mínus nám hovorí, že  má opačný smer ako je  kladná x-ová os . Ako už vieme,  udáva dostredivé zrýchlenie.

Pre výslednú veľkosť absolútneho zrýchlenie mravca vzhľadom na gramofón, pri zvážení sčitovania dvoch navzájom kolmých vektorov, dostávame

 

 

Po číselnom dosadení

 

 

 

Smer vektora a určíme opäť pomocou niektorej z trigonometrických funkcií, napríklad pomocou odklonu b od y-ovej osi

 

 

Po číselnom dosadení dostaneme

 

 

Ak chceme vyjadriť smer vektora zrýchlenia uhlom a platí

 

a = 90 ⁰ + b  = 179 ⁰

 

 

Rýchlosť mravca pohybujúceho sa po točiacej sa gramafónovej platni vzhľadom na pevnú sústavu spojenú s gramafónom v okamžiku t =10 s má veľkosť v = 1,257 m.s^-1   a  smer určený  odklonom od pôvodného smeru rýchlosti  v počiatočnom okamžiku ( od x-ovej osi ) o uhol a   = 89 ⁰ .

Absolútné  zrýchlenie v okamžiku t =10 s má veľkosť a = 15,79  m.s^-2 a  smer určený  odklonom od pôvodného smeru rýchlosti  v počiatočnom okamžiku ( od x-ovej osi ) o uhol  a =  179 ⁰ .

 

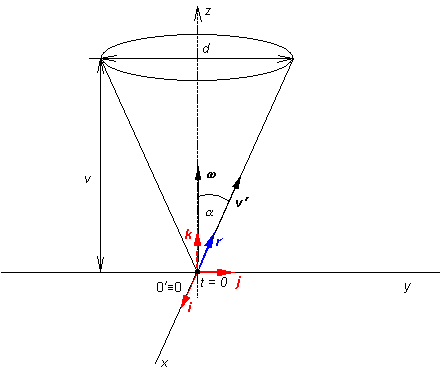
Príklad 2.1.17

Po nádobe tvaru rotačného kužeľa s priemerom d a výškou v, rotujúcej okolo osi prechádzajúcej osou kužeľa konštantnou uhlovou rýchlosťou w sa pohybuje chrobáčik rovnomernou rýchlosťou v smere povrchovej priamky tak, že v čase t = 0  práve vychádza z vrcholu. Určite veľkosť absolútnej rýchlosti  a veľkosť absolútneho zrýchlenia chrobáčika vzhľadom na pevné okolie v čase t od začiatku pohybu.

 

 

Z rozboru zadania príkladu vyplývajú nasledovné skutočnosti:

·      Chrobáčik pohybujúci sa po povrchovej priamke kužeľa možno považovať za pohyb v relatívnej sústave, ktorá sa vzhľadom na okolie otáča konštantnou uhlovou rýchlosťou w.

·      Počiatky obidvoch sústav zvolíme do spoločného bodu , ktorým je vrchol kužeľa . Vektor uhlovej rýchlosti w orientujme do osi z, t.j. w = ( 0, 0, w).

·      Polohový vektor r´ určujúci polohu chrobáčika v relatívnej sústave (vzhľadom na sústavu pevne spojenú s kužeľom) je v našom prípade totožný s polohovým vektorom r v absolutnej sústave pevne spojenej s okolím, t.j. r´= r .

·      Použijeme  všeobecné vzťahy pre rýchlosť a zrýchlenie pre zložený pohyb (2.1.127) a (2.1.131)

       

 v   =   v₀  + v´ + (w ´ r´)

 

a    = a´ +  2 (w ´ v´)  + w  ´ (w ´ r´)  +  a ´  r´

 

·      Zo zadania príkladu vyplýva, že vo výraze pre rýchlosť  člen v₀  je nulový, kým pre zrýchlenie sú nulové prvý a štvrtý člen, nakoľko počiatok sústavy relatívnej sa nepohybuje vzhľadom na absolútnu   sústavu a    relatívna sústava - kužeľ,    rotuje konštantnou   uhlovou  rýchlosťou, takže a  = 0.

Takže vychádzajúcimi vzťahmi sú nasledovné rovnice

 

     v   =  v´ + (w ´ r´) = v´ + (w ´ v´t

 

     a    =   2 (w ´ v´)  + w  ´ (w ´ r´) 

 

    Z vlastností vektorového súčinu vidíme, že vektory v´  a  (w ´ v´t) sú navzájom kolmé a taktiež vektory     2 (w ´ v´)  a  w  ´ (w ´ r´) sú taktiež kolmé.

·      veľkosť vektora   |w ´ v´t | = (w v´t) sin a

·      uhol a je uhol medzi vektorom  w  a  v´, pre ktorý platí :

     

   

 

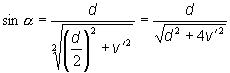
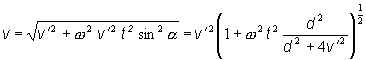
            | a |  = ( |2 (w ´ v´)  | ²   +  |  w  ´ (w ´ r´) | ² )^1/2

 

 

 

 

 

_____________________________________________

 

Kontrolné otázky k časti 2.1.6

 

1.     Kedy hovoríme o zloženom pohybe?

2.     Z akých pohybov sa skladá zložený pohyb?

3.     Koná dažďová kvapka zložený pohyb ak: a) nefúka vietor, b) ak fúka silný bočný vietor?

4.     Kedy hovoríme o derivácii fyzikálnej veličiny absolútnej?

5.     Kedy hovoríme o derivácii fyzikálnej veličiny relatívnej?

6.     Napíšte súvis medzi absolútnou a relatívnou deriváciou zvolenej fyzikálnej veličiny.

7.     Sú jednotkové vektory karteziánskej súradnicovej sústavy vždy konštantné?

8.     Z akého dôvodu musíme rozlišovať deriváciu absolútnu a relatívnu?

9.     Napíšte vzťah pre deriváciu jednotkového vektora, ktorého veľkosť je konštantná, ale  smer sa mení.  

10.  Vyjadrite rýchlosť hmotného bodu A vzhľadom na absolútnu sústavu. Vysvetlite význam jednotlivých veličín i členov.

11.  Vyjadrite rýchlosť hmotného bodu A vzhľadom na relatívnu sústavu. Vysvetlite význam jednotlivých veličín i členov.

12.  Vyjadrite zrýchlenie hmotného bodu A vzhľadom na absolútnu sústavu. Vysvetlite význam jednotlivých veličín i členov.

13.  Vyjadrite zrýchlenie hmotného bodu A vzhľadom na relatívnu sústavu. Vysvetlite význam jednotlivých veličín i členov.

14.  Napíšte vzťah pre Coriolisove zrýchlenie.

15.  Kedy musíme zvažovať pôsobenie Coriolisovho zrýchlenia? Uveďte príklady.