2.6.6 Dilatácia časového intervalu

Majme hodiny, ktoré merajú čas pomocou svetelného lúča. Jedna časová jednotka  (jeden „tik“) nech sa rovná dobe, počas ktorej svetelný lúč vyslaný z bodu A prejde do bodu B,( AB=L) , kde sa odrazí a vráti sa späť do bodu A:  t₀ = 2 L/c.

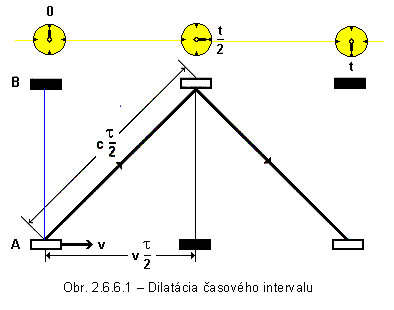
Hodiny uložené v smere osi y vložme do rakety ako na obr. 2.6.6.1, ktorá sa pohybuje od Zeme rýchlosťou v v smere osi x. Pozorovateľ na Zemi odmeria časovú jednotku t, počas nej lúč prejde dráhu

 

ct  a súčasne raketa sa v smere osi x posunie o dráhu nt:

 

 

odkiaľ po úprave

 

 

a po predelení čitateľa a menovateľa  c² a odmocnení máme výsledok.

 

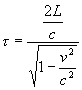
Teda:

 

                                                                                                    (2.6.6.1 )

 

Vzťah (2.6.6.1 ) definuje dilatáciu časového intervalu. Najmenší časový interval nameriame v sústave, vzhľadom na ktorú sú hodiny v pokoji. Vo všetkých sústavách, ktoré sa vzhľadom na hodiny pohybujú, nameriame väčší časový interval.

 

 

Príklad 2.6.6.1: Astronaut v kozmickej lodi nameral dobu svojho letu 30 rokov. Rýchlosť lode vzhľadom na Zem je 0,8c. Koľko rokov uplynie medzitým na Zemi ?

 

Riešenie:

Označme dobu pohybu astronauta v lodi t_o= 30 rokov a rýchlosť, ktorou sa pohybuje loď v =0,8c. Vyjdeme zo vzťahu (2.6.6.1 ) :

 

   

 

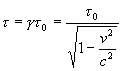
 dosadením dostávame :

                     

 

 

 

 

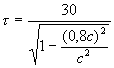
Na Zemi počas 30-ročného letu astronauta v rakete uplynie 50 rokov.