2.6.4 Relativita súčasnosti

                   Topic 4

     Uvažujme dve udalosti, ktoré sa odohrali v sústave S v bodoch x_A  a x_B   v časových okamihoch  t_A  a  t_B . Časový interval medzi udalosťami v sústave S je t_B - t_A. Zistíme aký bude tento interval v sústave S´:

 

 ,                                                                       (2.6.4.1)

 

keď sme použili prvý z transformačných vzťahovc1010 (2.6.3.4)  a

 

.

 

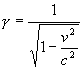Je vidieť, že ak by sa udalosti A a B v nečiarkovanej sústave udiali súčasne (t. j. t_B – t_A = 0), pozorovateľ v čiarkovanej sústave nameria medzi nimi časový interval rôzny od nuly, teda preňho nie sú súčasné. Iba v prípade, že udalosti v nečiarkovanej sústave sa udejú súčasne a naviac v jednom mieste, t.j. súmiestne (x_B – x_A = 0),  budú aj pre pozorovateľa v čiarkovanej sústave súčasnými.Vtedy však nepôjde o dve, ale iba o jednu bodovú udalosť.

 

 

Príklad 2.6.4.1  V súradnicovej sústave S spojenej so stálicou, udalosť  B nasledovala o jednu sekundu neskôr ako udalosť A, ktorá sa udiala v mieste vzdialenom od B o 6.10⁵ km. Akou rýchlosťou sa musí pohybovať raketa, aby astronaut pozoroval udalosti A a B ako súčasné?

Riešenie: Označme vzdialenosť medzi udalosťami A a B  d = x_B - x_A = 6.10⁵ km  a časový interval l udalostí  t_B – t_A = 1 s. Zo zadania  vyplýva podmienka, že obidve udalosti A a B, musia byť súčasné, teda pomocou vzťahu (2.6.4.1) dostávame:

 

 

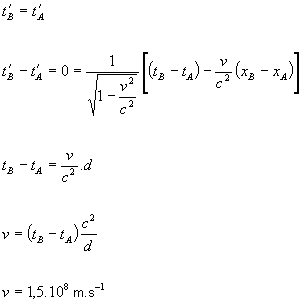
Raketa sa musí pohybovať rýchlosťou 1,5.10⁸ ms^-1 , aby astronaut pozoroval udalosti A,B ako súčasné.

 

Zistíme teraz, ako to bude s časovým poradím príčiny a následku pri prechode z jednej do druhej súradnicovej sústavy. Nech v čiarkovanej sústave udalosť B je príčinou udalosti A, teda časový interval na ľavej strane rovnice (2.6.4.1) je kladný (udalosť A nastáva po udalosti B). Aký bude časový interval t_B - t_A? Upravme (2.6.4.1) tak, že uvedený interval vyberieme pred zátvorku a postupne dostávame:

 

 

kde

 

 

je rýchlosť šírenia sa informácie, teda

 

 

a ak

   ,

posledný dvojčlen na pravej strane je kladný a teda ak ľavá strana predchádzajúcej rovnice je kladná (ako sme predpokladali), z toho vyplýva, že aj interval t_B - t_A  je kladný a teda aj v nečiarkovanej sústave príčina predchádza následok.

V žiadnej sústave nemôže nastať zámena časového poradia príčiny a následku. Podmienka

  

 je nutnou a postačujúcou podmienkou pre platnosť princípu kauzality: následok vždy nasleduje po príčine. Vzájomné pôsobenie (interakcia) medzi materiálnymi objektmi môže prebiehať iba menšími, nanajvýš rovnakými rýchlosťami u ako je rýchlosť svetlac1170 c. Za tejto podmienky je teda špeciálna teória relativity v súlade s princípom kauzality.