2.6.3 Postuláty špeciálnej teórie relativity a Lorentzove transformácie

 

     Špeciálnu teóriu relativity vybudoval v roku 1905 Albert Einstein na základe dvoch postulátovc1190:

1. Rýchlosť svetlac1170 vo všetkých inerciálnych sústaváchc1160 je rovnaká (ak by nebola, v predošlom pokusec1005 by sa  bol nameral posun).

2.Všetky inerciálne sústavy sú rovnocenné, žiadna z nich nie je preferovaná, teda neexistuje absolútna vzťažná sústava. Fyzikálne zákony,  pri prechode z jednej inerciálnej sústavy do druhej sa nemenia, teda sú  invariantné. (Ani pomocou mechanických, ani pomocou optických dejov nie je možné zistiť absolútny pohyb inerciálnej sústavy, čo tiež vyplynulo z negatívneho výsledku pokusu).

Hoci na prvý pohľad tieto postuláty nevyzerajú prevratne, ako uvidíme z ich dôsledkov, menia v skutočnosti takmer všetky intuitívne vytvorené predstavy o priestore a čase.

 

   

 V súlade s uvedenými dvomi Einsteinovými postulátmi nahradíme Galileiho transformáciec1000 všeobecnejšími Lorentzovými transformáciami.

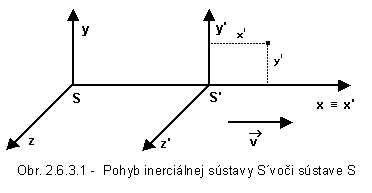
Majme dve sústavy  S a S´, kde y = y´, z = z´ a  čiarkovaná sústava sa pohybuje

konštantnou rýchlosťou v v kladnom smere osi x. Vhodný odhad tvaru závislosti x a x´ je:

 

                                                                                                             (2.6.3.1)

 

kde g je kladný parameter, lebo predpokladáme súhlasnú orientáciu osí x a x´, ktorý nezávisí od x a t, ale môže byť funkciou rýchlosti v.

Voľba závislosti (2.6.3.1) má niekoľko dôvodov:

- vzťah (2.6.3.1) je lineárny, takže každá jednotlivá udalosť v nečiarkovanej sústave odpovedá   určitej jednotlivej udalosti v čiarkovanej sústave (ako to má byť)

- je jednoduchý a je samozrejmé, že vždy treba hľadať, čo najjednoduchšie riešenie

- dá sa redukovať na Galileove transformácie súradníc (pre ).

 

Z podmienky rovnocennosti S a S´ (2. postulát) vyplýva, že inverzná transformácia S ® S¢  sa od transformácie S¢ ®  S odlišuje iba znamienkom rýchlosti v, takže súčasne s (2.6.3.1) platí:

 

                                                                                                            (2.6.3.2)

 

Ak v čase t = t´= 0 s  sa zo spoločného (v tom okamihu) počiatku S a S´ vyšle svetelný signál v smere osi x, ten sa šíri v smere x a x´ podľa rovníc:

 

x = ct,   x´= ct´   (podľa 1. postulátu)  Þ  t = x/c,   t´= x´/c .

 

Do (2.6.3.1) a (2.6.3.2) dosadíme za t a t´:

,

 

vzájomným vynásobením

 

,

 

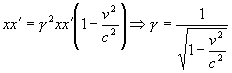teda:

 

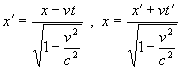                                                                                       (2.6.3.3)

 

Úpravou druhej z týchto rovníc, keď za x‘ dosadíme z prvej rovnice, dostaneme vzťahy pre transformáciu  časovej súradnice:

 

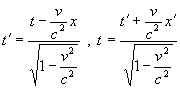                                                                                       (2.6.3.4)

 

Z týchto rovníc vyplýva, že časový interval nie je absolútna veličina, ako aj to, že priestor a časový interval nie sú nezávislé.

 

Rovnice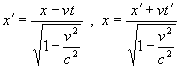               

 

                               y‘ = y

                               z‘ = z

 

                                          

 

 

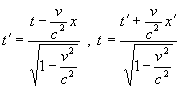
predstavujú Lorentzove transformácie priestorových súradníc a časovej súradnice pre inerciálne sústavy, pohybujúce sa vzájomne rýchlosťami blízkymi rýchlosti svetla.c1170

Všetky transformačné rovnice majú zmysel iba pre v < c. Pri malých rýchlostiach v prechádzajú Lorentzove transformácie na Galileove – tam platí klasická fyzika.