2.6

 

ŠPECIÁLNA TEÓRIA RELATIVITY

2.6.1 Galileiho transformácie

 

Na začiatok si uvedieme príklad inerciálnej sústavyC1160. Napr. rovnomerne priamočiaro sa pohybujúci železničný vozeň, ktorý budeme v istom priblížení považovať za inerciálnu sústavu. Všetky deje prebiehajú rovnako ako na zemskom povrchu. Ak je guľôčka, ktorá je vo vozni, bez pôsobenia síl v pokoji, ostane v pokoji. Keď sa ale vozeň dá do zrýchleného pohybu (t.j. mení veľkosť alebo smer rýchlosti), guľôčka sa začne pohybovať, hoci žiadna vonkajšia sila na ňu nepôsobí. Teraz vagón vytvára neinerciálnu súradnicovú sústavu. Ak by sme sústavu viazanú na Zem považovali za inerciálnu, potom sústava viazaná na vagón je už neinerciálna. Newtonove pohybové zákonyc1165  platia v známom tvare iba v inerciálnych sústavách (sústavy, ktoré sú v pokoji alebo rovnomernom priamočiarom pohybe).

 

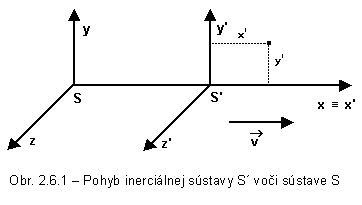
Majme dve inerciálne súradnicové sústavy s počiatkami S a S´, ktoré v čase t = 0s sú v spoločnom počiatku S. Čiarkovaná sústava nech sa pohybuje  rovnomerným priamočiarym pohybom v smere osi x konštantnou rýchlosťou v.

 

 

Pre prechod z jednej inerciálnej sústavy do druhej slúžia Galileiho transformácie:

 

                                                                                 (2.6.1.1)

 

2. Newtonov pohybový zákon zapíšeme v zložkovom tvare:

 

 

 

pri prechode z S do S´ platí:

 

 

teda potom

 

 

t.j. F´=F, čo znamená, že 2. Newtonov pohybový zákon platí v rovnakom tvare v každej inerciálnej sústave.

 

Galileiho princíp relativity hovorí, že pohybové zákony sú invariantné*[1]  vzhľadom na Galileiho transformácie. To znamená, že mechanické deje prebiehajú vo všetkých inerciálnych sústavách podľa rovnakých zákonov. Pozorovaním mechanických javov vnútri danej inerciálnej sústavy nie je možné zistiť jej pohyb (rovnomerný priamočiary), ani jej rýchlosť. Z hľadiska mechaniky sú takto všetky inerciálne sústavy na popísanie pohybu rovnocenné. Ukázalo sa, že keď sa pomocou Galileiho transformácií prechádza z jednej inerciálnej sústavy do druhej pri popise elektromagnetických dejov, mení sa tvar rovníc, ktoré ich popisujú, teda nie sú invariantné. Ak to tak naozaj je – rovnice nie sú invariantné, potom pomocou elektromagnetických dejov, napr. elektromagnetického žiarenia, by sa dal pozorovať pohyb inerciálnej sústavy. Ak to tak nie je a teda pohyb sa pozorovať nedá (rovnice sú invariantné), potom v prípade veľkých rýchlostí,c1170 ktorými sa šíri elektromagnetické žiarenie, už nevyhovujú Galileiho transformácie a treba nájsť nové transformácie. Existoval  teda problém, k riešeniu ktorého značnou mierou prispel Michelsonov – Morleyov pokus.