3.3.4         Tlak pod zakriveným povrchom

 

Konkávne zakrivený povrch (vypuklý) tlačí na kvapalinu viac ako konvexný povrch (vydutý). Dodatočný tlak, ktorý vzniká vplyvom zakrivenia povrchu sa volá kapilárny tlak. Kapilárny tlak sa pripočíta ku kohéznemu tlaku ak je povrch vypuklý a odpočíta sa ak je povrch vydutý. Výslednica molekulových síl je teda pri vydutom povrchu väčšia. Tlak vo vnútri bubliny je preto vždy väčší, ako vonkajší tlak.

Určime kapilárny tlak na jednoduchom príklade guľovej kvapky s polomerom r. Práca, ktorú by vykonali povrchové sily pri zmenšení povrchu kvapky o dS vedie k zmenšeniu povrchovej energie o dE = s dS. Táto sa musí rovnať práci na zmenšenie objemu o dV pri kapilárnom tlaku p_k:  dW = p_k dV.  Pre diferenciály povrchu a objemu gule platí:

dS = 8 p r dr a dV= 4 p r² dr.

 

Potom

 

 

 

a  pre  kapilárny tlak dostávame:

 

                                                                                                                    (3.35)

 

V bubline vytvorenej napríklad z mydlového roztoku sú zakrivené povrchy dva, a tlak v mydlovej bubline je väčší ako vonkajší tlak o dvojnásobok p_k. Tlak v bubline:

 

                                                                                                          (3.36)

 

Vo všeobecnosti môžeme zakrivený tvar povrchu charakterizovať pomocou polomerov dvoch na seba kolmých kružníc. Pre kapilárny tlak potom platí Laplaceov vzťah:

 

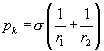                                                                                                         (3.37)

 

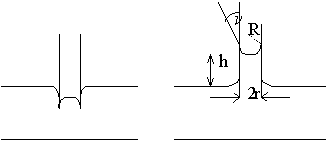
Pri ponorení úzkej trubice do kvapaliny sa vytvorí zakrivený povrch kvapaliny v trubici. Podľa toho, či kvapalina zmáča steny trubice, alebo nie, bude zakrivený povrch vydutý, alebo vypuklý.

 

Obr. 3.28

 

Ak  kvapalina  zmáča  steny trubice vzniká kapilárne zvýšenie kapilárna elevácia.   Tlak pod zakriveným povrchom bude totiž menší o

                     ,

kde R je polomer krivosti vzniknutého menisku v kapiláre. Prevaha vonkajšieho tlaku potom vytláča kvapalinu v kapiláre nahor a to  dovtedy,  kým sa zníženie tlaku nebude rovnať hydrostatickému tlaku zdvihnutej kvapaliny. Pre výšku stĺpca kvapaliny - tzv. elevačnú výšku, potom platí:  

 

                                                                                                                   (3.38)

 

Kapilárna elevácia poskytuje takto jednoduchú metódu na určenie povrchového napätia.

            Opačný jav je kapilárna depresia. Dochádza k nej vtedy, keď sa kvapalina snaží zo steny kapiláry stiahnuť. Povrch kvapaliny bude vypuklý a tlak v kvapaline o kapilárny tlak väčší. Hladina kvapaliny v kapiláre poklesne.

 

––––––––––––––––––––––––––––––––––––––

Príklad 3.17  Do vody sú ponorené dve sklené kapiláry s polomermi r₁ = 1 mm, r₂ = 1,5 mm. Vypočítajte povrchové napätie, keď rozdiel hladiny vodných stĺpcov v týchto kapilárach je 4,9 mm a keď predpokladáme, že voda dokonale zmáča steny sklenej trubice.

 

Riešenie:  Kapilárna elevácia vody v kapiláre vytlačí stĺpec vody do výšky

 

.

 

Polomer zakrivenia kvapaliny v kapiláre môžeme vyjadriť:

             

 

kde r je polomer kapiláry, υ je krajný uhol  (obr. 3.28) - teda uhol, ktorý zviera voda so stenou kapiláry, ρ je hustota vody. Ak voda dokonale zmáča stenu, bude R = r . Rozdiel výšok hladín pri dvoch rôznych kapilárach s polomermi r₁a r₂ bude:

 

.

 

 Odtiaľ dostaneme pre povrchové napätie:

 

                               

–––––––––––––––––––––––––––––––––––––––––