3.1.3  Tlak v stlačiteľnej tekutine

V prípade, že tekutina je významne stlačiteľná, napr. plyny, potom pre integráciu rovnice (3.9)  potrebujeme poznať závislosť hustoty na tlaku. Hľadajme napríklad závislosť tlaku vzduchu od výšky, za predpokladu konštantnej gravitačnej sily a teploty. Z rovnice ideálneho plynu pri konštantnej teplote platí

 

 

konšt., kde p₀ a r₀ je tlak a hustota na referenčnej hladine. Po dosadení za hustotu a

 

malej úprave má potom rovnica ( 3.9) tvar:

 

                                                                                                           (3.12)

 

Rovnicu budeme integrovať v odpovedajúcich hraniciach:

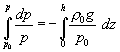                                                                                                     (3.13)

 

a dostávame závislosť tlaku od výšky:

 

                                                                      (3.14)

 

Tlak vzduchu konštantnej teploty v závislosti od výšky exponenciálne klesá.

 

––––––––––––––––––––––––––––––––––––––

Príklad 3.5  Vypočítajte tlak vzduchu vo výške  h = 10 000 m nad hladinou mora.

Riešenie: Zo stavovej rovnice:

 

konšt., pre závislosť hustoty vzduchu od tlaku pri konštantnej teplote platí: 

 

 

konšt.,  kde  p_o = 1,01325.10⁵ Pa je  atmosférický  tlak  na  hladine  mora, r_o = 1,29 kg m^–3  je hustota vzduchu pri tomto tlaku.

 

 

Dosadením týchto hodnôt do odvodenej rovnice (3.14) dostaneme, že tlak vzduchu vo výške 10 km bude p = 2,9.10⁴ Pa.

––––––––––––––––––––––––––––––––––––––