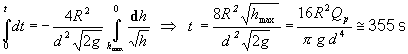3.2.4       Výtok kvapaliny otvorom malého prierezu

 

Majme kvapalinu hustoty r v širokej otvorenej nádobe, na dne ktorej je malý otvor (obr.3.19).

 

 

 

 

 

 

 

 

 

           

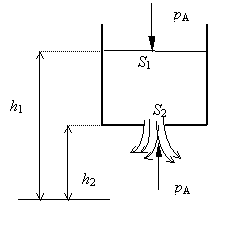
Obr.3.19

 

Tlak v prierezoch S₁ aj S₂ je rovnaký a rovná sa atmosférickému tlaku. Bernoulliho rovnica pre miesta 1 a 2 má tvar:

 

                                                                  (3.21)

 

Platí S₁ >> S₂, preto v₁ << v₂ a kinetickú energiu objemovej jednotky v mieste 1 môžeme zanedbať oproti kinetickej energii v mieste 2. Pre rýchlosť výtoku kvapaliny dostávame:

 

                                                                                                     (3.22)

 

Rozdiel h₁ – h₂ = h je výška kvapaliny nad otvorom. Vzťah, ktorý sme odvodili pre rýchlosť výtoku ideálnej kvapaliny otvorom malého prierezu

     sa volá Toricelliho vzťah.

Poznámka: Všimnite si, že rýchlosť výtoku ideálnej kvapaliny je taká istá, ako by bola rýchlosť telesa padajúceho z rovnakej výšky. Rýchlosť výtoku reálnych kvapalín bude v dôsledku viskozity menšia.

––––––––––––––––––––––––––––––––––––––

Príklad 3.12 Nádoba postavená na vodorovnej rovine je naplnená vodou do výšky  h = 0,4 m a udržuje sa na tejto hladine. Ako vysoko nad dnom musíme urobiť v stene nádoby otvor, aby voda striekala čo najďalej na vodorovnú rovinu? (obr. 3.20)

 

Riešenie:

 

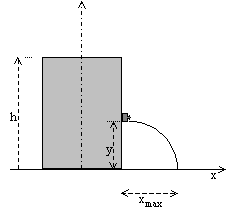
Obr. 3.20

                                                                     

 

 

Pre jednotlivé častice kvapaliny pri vytekaní z otvoru platia kinematické rovnice opisujúce vodorovný vrh:

 ,

pričom pre výtokovú rýchlosť platí Torricelliho vzťah:

 

.

 

Po dosadení rýchlosti  v a času  t, pre súradnicu  x dostaneme:                                                                        

 

 

Hľadáme extrém tejto funkcie, teda:

 

 

 

Príklad 3.13  Valcový rezervoár na vodu s polomerom R = 50 cm má na dne otvor s priemerom  d = 4 cm. Do nádoby priteká voda s objemovým tokom Q_p = 0,7.10^–2 m³.s^–1. Akú maximálnu výšku dosiahne voda v rezervoári? Ako dlho bude trvať jeho vyprázdnenie, ak sa prítok vody zastaví v čase, keď hladina vody je maximálna?

 

Riešenie: 

Ustálenú maximálnu výšku vody v rezervoári dostaneme, ak sa prítok vody Q_p rovná výtoku Q_v:    

 

 

 

pričom sme za výtokovú rýchlosť dosadili Torricelliho vzťah.

Po uzavretí prítoku bude sa výtok rovnať časovému úbytku objemu vody z rezervoára:

 

  ,

kde  V = S_V h = p R² h  ,

 

pričom 

.

 

Po dosadení dostaneme:

 

 .

 

Separáciou premenných a integráciou: